Aufgabe:
2. Zeichnen Sie die Graphen der Funktionen \( \mathrm{g}_{1} \) bis \( \mathrm{g}_{4} \) in ein Koordinatensystem. Wählen Sie als Zeichenbereich \( -5 \leq y \leq 5 \) und \( -5 \leq x \leq 5 \)
a) \( g_{1}: y=2 x-3 \)
b) \( g_{2}: \mathrm{y}=-\frac{1}{2} \mathrm{x}+4 \)
c) \( g_{3}: \mathrm{y}=\frac{9}{10} \mathrm{x}-2 \)
d) \( g_{4}: y=-2 x-8 \)
Hinweis zu d): Jeder Punkt einer Geraden kann als Ausgangspunkt für ein Steigungsdreieck dienen!
3. Bestimmen Sie die Koordinaten des Schnittpunkts der Funktionen \( g_{1} \) und \( g_{2} \) und markieren Sie ihn in ihrer Zeichnung!
4. Bestimmen Sie die Nullstelle von \( \mathrm{g}_{2} \).
5. Zeigen Sie durch Rechnung, dass \( \mathrm{P}(5 \mid 2,5) \) auf \( g_{3} \) liegt, \( Q(1|3) \) aber nicht auf \( g_{2} \).
Ansatz:
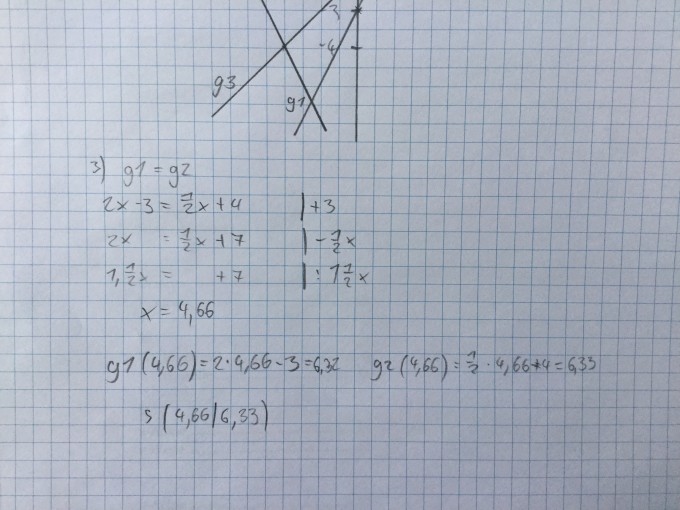
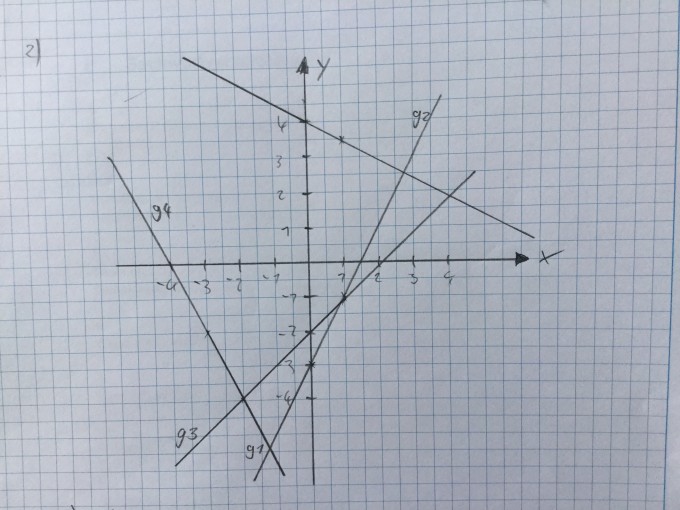
Was habe ich falsch gemacht bei mir kommt (4,66 | 6,33) raus, dass haut nach meiner Zeichnung ja aber nicht hin.
Nachtrag: g2 ist die obere Linie.