Bestimmen Sie die Koordinaten des Schnittpunkts der Funktion g1 und g2.

Question

Aufgabe:

2. Zeichnen Sie die Graphen der Funktionen $\mathrm{g}_{1}$ bis $\mathrm{g}_{4}$ in ein Koordinatensystem. Wählen Sie als Zeichenbereich $-5 \leq y \leq 5$ und $-5 \leq x \leq 5$

a) $g_{1}: y=2 x-3$
b) $g_{2}: \mathrm{y}=-\frac{1}{2} \mathrm{x}+4$
c) $g_{3}: \mathrm{y}=\frac{9}{10} \mathrm{x}-2$
d) $g_{4}: y=-2 x-8$

Hinweis zu d): Jeder Punkt einer Geraden kann als Ausgangspunkt für ein Steigungsdreieck dienen!

3. Bestimmen Sie die Koordinaten des Schnittpunkts der Funktionen $g_{1}$ und $g_{2}$ und markieren Sie ihn in ihrer Zeichnung!

4. Bestimmen Sie die Nullstelle von $\mathrm{g}_{2}$.

5. Zeigen Sie durch Rechnung, dass $\mathrm{P}(5 \mid 2,5)$ auf $g_{3}$ liegt, $Q(1|3)$ aber nicht auf $g_{2}$.

Ansatz:

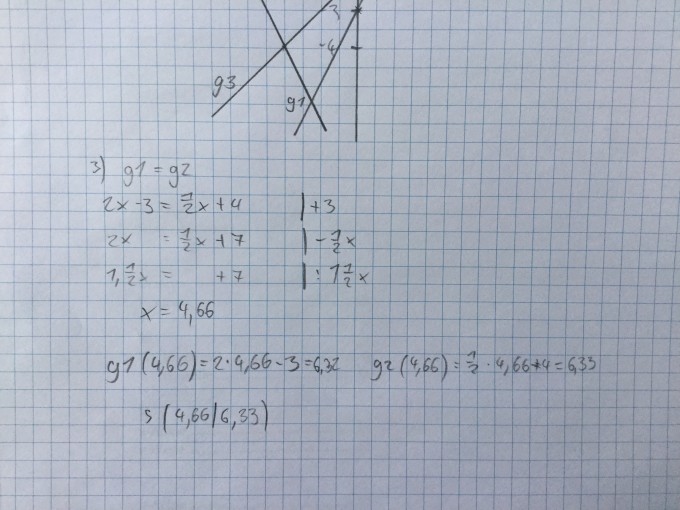
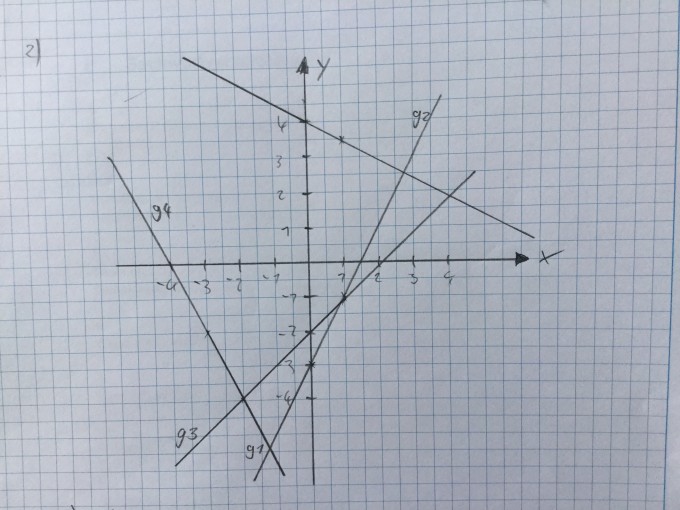
Was habe ich falsch gemacht bei mir kommt (4,66 | 6,33) raus, dass haut nach meiner Zeichnung ja aber nicht hin.

Nachtrag: g2 ist die obere Linie.

Answer 1

Du hast ein Minuszeichen unterschlagen

$$2x-3= \colorbox{#ffcccc}{-}\frac12 x +4$$

$$2x= \colorbox{#ffcccc}{-}\frac12 x +7$$

$$2x= \colorbox{#ffcccc}{-}\frac12 x +7 \quad \left| \colorbox{#ffcccc}{+} \frac12 x\right.$$

$$\frac{ \colorbox{#ffcccc}{5} }{ \colorbox{#ffcccc}{2} } x = 7$$

$$x=\frac{14}{5}=2,8 \quad y= 2 \cdot \frac{14}{5} - 3 = \frac{13}{5}=2,6$$

Comments

 Ist das richtig so. (Nulstelle bestimmen von g2)

---

Ja - das ist völlig richtig!

---

Ein Tipp noch: Du kannst hier auch den 'Plotlux Plotter' für Funktionen benutzen (rechts auf dieser Seite unter 'Mathe-Tools:') - sieht dann so aus:

Plotlux öffnen

f₁(x) = 2x-3f₂(x) = -x/2+4f₃(x) = 9x/10-2f₄(x) = -2x-8Zoom: x(-5…6) y(-6…5)

---

hallo,

ich weiß, die Frage ist schon etwas her. Da ich aber an der selben Aufgabe sitze hab ich eine Anmerkung: Hier wurde die Nullstelle von g1 berechnet. g2 ist y=-1/2x +4

Also:

-1/2x+4 = 0    l -4

-1/2x = -4      l : -1/2

x = 8