Hallo Secret123! :-)
Ansatz: f(x) = A·sin(b(x + c)) + d
Die Funktion pendelt um die Ruhelage d=0 mit einem maximalen Ausschlag y=5 in positiver und y = -5 in negativer Richtung. Damit ist die Amplitude A=5, denn das ist der höchste Ausschlag bezogen auf die Ruhelage. Wir haben von t=3 bis t=10 eine halbe Periode T/2 = 10-3 = 7.
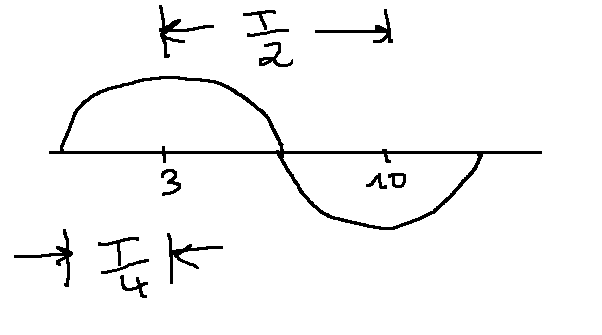
Eine ganze Periode ist T=14. und die Kreisfrequenz ω = 2π/T = π/7.
Eine Viertelperiode ist demnach T/4 = 7/2 = 3,5.
Da nach einer Viertelperiode der Ausschlag bei t=3 maximal ist, haben wir
eine Nullstelle bei t=-0,5(Linksverschiebung) d.h. den Parameter c = 0,5.
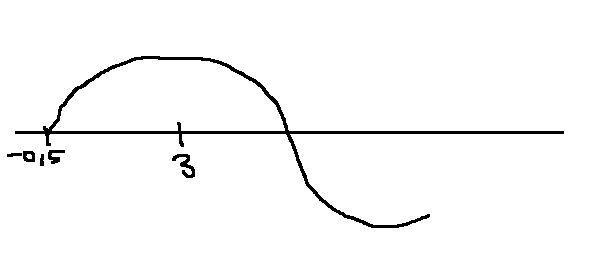
Mit dem Ansatz f(x) = A·sin(b(x + c)) + d bekommen wir
y = 5*sin( π/7 (x + 0,5))
Bzw. für y=Asin(ωt+φ) ist
φ = π/7*0,5 = π/7* 1/2 = π/14 ==>
y = 5 sin(π/7 t + π/14)
Grüße