Hallo Sophie,
zu (a) 1.) aus der 'Regelmäßigkeit' folgt, dass das Fünfeck nach jeder Drehung um \(2\pi/5 = 72°\) wieder auf sich selbst abgebildet wird, und damit sind auch alle Diagonalen deckungsgleich - und damit gleich lang.
2.) Alle Innenwinkel der regelmäßigen Fünfecks betragen \(108°\). Alle Seiten sind gleich lang. Nach dem Konkruenzaxiom SWS (2 Dreiecke sind kongruent, wenn zwei Seiten und der eingeschlossene Winkel gleich sind) ist auch die dritte Seite - und damit die Diagonale - immer gleich lang.
zu (c) ich ziehe (c) vor, da mit der Aussage von (c) sich (b) leicht beweisen lässt.
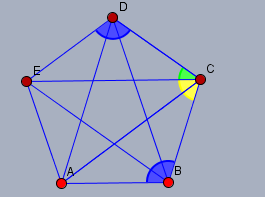
Der Winkel \(CDE=108°\) (blau). Das Dreieck \(ECD\) ist ein gleichschenkliges, da \(CD=DE\); folglich ist der Winkel \(ECD\) (grün) \(\angle ECD = \frac12 (180°-108°)=36°\). Der Winkel \(BCE\) (gelb) ist \(\angle BCE = 108°-36°=72°\). Die Summe der Winkel \(\angle ABC= 108°\) und \(\angle BCE=72°\) ergibt \(180°\). Daraus folgt, das die Gerade durch \(AB\) parallel zu der Geraden durch \(CE\) liegt. Damit ist das Viereck \(ABCE\) ein Trapez.
zu (b) Du hast den Punkt \(F\) nicht eingezeichnet, aber ich gehe davon aus, dass er auf der Diagonalen \(EC\) liegt.
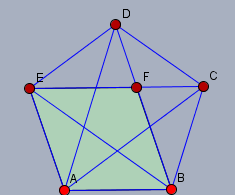
Und es soll bewiesen werden, dass das Viereck \(ABFE\) ein Rhombus ist. In (c) ist bereits bewiesen, das jede Seite parallel zu der Diagonalen liegt, die keine gemeinsamen Eckpunkte des Fünfecks mit der Seite hat. Daraus folgt bereits, dass das Viereck \(ABFE\) ein Parallelogramm ist, da \(AB \parallel EC\) und \(EA \parallel BD\). Da die Seiten \(AB\) und \(EA\) gleich lang sind, ist \(ABFE\) auch ein Rhombus.
Gruß Werner