Diagonalenschnittpunkt M Rhombus Beweis

Question

Wie Beweist man das?

Vom Diagonalenschnittpunkt M eines Rhombus / einer Raute ABCD werden Lote auf die Seiten gefällt.

Beweise, dass die Fußpunkte dieser Lote ein Rechteck bilden.

Answer 1

Aus Symmetriegründen genügt die Betrachtung eines Viertelrhombus:

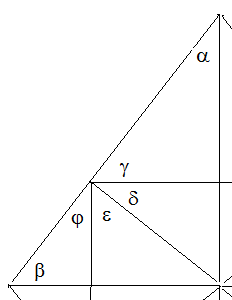
hier gilt: γ=90°-α und φ=90°-β. Addition ergibt γ+φ=180°-(α+β). Da α+β=90° ist also γ+φ=90°. Da γ+δ+ε+φ=180° ist δ+ε=90°.An jedem Lotfußpunkt liegt also ein rechter Winkel. Ein Viereck mit vier rechten Winkeln ist ein Rechteck.

Answer 2

Benütze die Symmetrieeigenschaften des Rhombus und schließe daraus auf die Symmetrien des entstehenden Fußpunkt-Vierecks !