Hallo Martin,
Die Schnittfläche die ein Zylinder aus einer Ebene heraus schneiet, ist eine Ellipse. Es reicht als aus die beiden Halbachsen der Ellipse zu bestimmen. Dazu folgende Skizze:
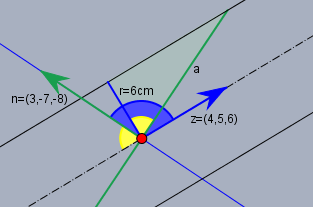
Die Zeichenebene sei die Ebene, in der sich sowohl der Normalenvektor \(n=(3,-7,-8)^T\) (grün) der Ebene als auch der Richtungsvektor \(z=(4,5,6)^T\) (blau) des Zylinders befinden. Dann liegt die kleinere Halbachse \(b\) senkrecht zur Zeichenebene und ist identisch zu \(r\). Der blaue Winkel \(\alpha\) ist der WInkel zwischen den beiden Vektoren. Er berechnet sich aus dem Skalarprodukt
$$\alpha = \arccos \left( \frac{n \cdot z}{|n| \cdot |z|} \right) = \arccos \left( \frac{-71}{\sqrt{77} \cdot \sqrt{122}} \right) \approx \arccos(-0,7325) \approx 137,1°$$Die größere Halbachse \(a\) berechnet sich aus dem markierten rechtwinkligen Dreieck. Allgemein gilt
$$| \cos \alpha | = \frac{r}{a}$$
In diesem konkretem Fall ist \(\alpha \approx 137,1° > 90°\) und damit ist \(\cos \alpha < 0\). Der gelbe Winkel \(\beta\) ist aber \(\beta = 180°-\alpha\). Und da \(\cos x = -\cos (180°-x)\) trifft obiger Zusammenhang auch bei Winkeln oberhalb von \(90°\) zu.
$$a = \frac{r}{|\cos \alpha|} \approx \frac{6 \text{cm}}{0,7325} \approx 8,191 \text{cm}$$
mit \(F=a\cdot b \cdot \pi\) erhält man dann den Flächeinhalt
$$F = 8,191 \text{cm}\cdot 6 \text{cm} \cdot \pi \approx 154,4 \text{cm}^2$$