Untersuchen Sie die folgenden Zahlenfolgen auf Konvergenz, und bestimmen Sie ggf. den Grenzwert

Question

Untersuchen Sie die folgenden Zahlenfolgen (a_n)∞_n=1 auf Konvergenz, und bestimmen Sie ggf. den Grenzwert:

a) a_n = (6n²-2n) / (n²+1)

b) a_n = n - √(n²-5n)

c) a_n = 5ⁿ / n⁵

d) a_n = sin(n²) / 3n

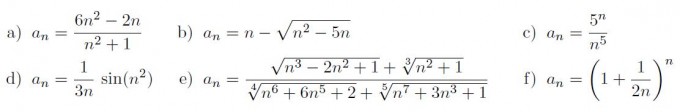
Hab selber schon einmal ein bisschen probiert, für a) habe ich 6 ermittelt, für b) 5/2, für c);d) habe ich 0 und mit e) und f) komme ich leider nicht zurecht und würde mich über eure Hilfe freuen und ob das was ich ermittelt habe in Ordnung ist. ;))

Answer 1

Bei c) würde ich +∞ sagen.

Bei f) ist es √e  . Schau mal dort https://de.wikipedia.org/wiki/Exponentialfunktion#Konvergenz_der_Folgendarstellung

Bei e) kannst du in jeder Wurzel die Potenz von n mit dem höchsten Exponenten ausklammern.

Das gibt dann   (   n^3/2*(.............)    +   n^2/3*(.............)     )    /    (   n^3/2*(.............)    +   n^7/5*(.............)     )

Der größte Exponent im Nenner ist 3/2 also alles mit  n^3/2  kürzen gibt :

(   1*(.............)    +   n^-5/6*(.............)     )    /    (   1*(.............)    +   n^-1/10*(.............)     )

Die mit den negativen Exponenten gehen gegen 0 . Die Klammern hinter den 1 Faktoren gehen gegen 1,

also insgesamt GW = 1.

Comments

danke für die Antwort!^^ Kannst du mir eventuell noch zeigen wie du auf c) kommst mit +∞ ?

---

Hab mal gelernt: Jede Exponentialfunktion mit Basis > 1 wächst

schneller als jede Potenzfunktion.

Answer 2

e) Schreibe von jedem Radikanden nur die höchste Potenz. Denn die bestimmt für große n den Wert der Folge, Hier (n(3/2)+n)/(n(3/2)+n(7/5)) und hier nur die größte Potenz im Zähler und im Nenner. Dann ist der Grenzwert 1.

f) Setze n=1/m und lasse m gegen 0 gehen. Dann ist der Grenzwert √e.