Fläche eines Dreiecks ...

Question

ich Blick da nicht durch.  Ich

Answer 1

Hallo Jibl,

Die IMHO einfachste Art, die Fläche zu berechenn läuft über das Kreuzprodukt $AB \times AC$. In jedem Fall muss man wissen, wo die Eckpunkte  $A$, $B$ und  $C$ liegen. Dazu setzt man in der gegebenen Gleichung zwei der drei Koordinaten =0 und berechet die dritte. Z.B. für $x$:

$$4x + 5y + 5z - 11= 0 \quad y=0; \space z=0; \quad \Rightarrow x=\frac{11}{4}$$

Daraus folgen dann die drei Punkte $A=(11/4;0;0)^T$, $B=(0;11/5;0)^T$ und $C=(0;0;11/5)^T$. Die Fläche ist dann

$$F =\frac12 \left| AB \times AC\right|=\frac12 \left| \begin{pmatrix} -11/4\\ 11/5\\ 0\end{pmatrix} \times \begin{pmatrix} -11/4\\ 0\\ 11/5\end{pmatrix} \right| \approx 4,915$$

Falls Du 'Kreuzprodukt' noch nicht gelernt hast, kann man sich hier auch zu Nutze machen, dass es ein gleichschenkliges Dreieck ist und der Mittelpunkt von $BC$ gleich dem Höhenfußpunkt $H_A$ ist.

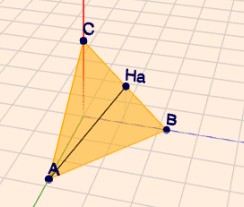
Die Fläche ergibt sich dann aus

$$BC= \begin{pmatrix} 0\\ -11/5\\ 11/5\end{pmatrix} \quad \Rightarrow |BC| \approx 3,111$$

$$AH_A= \begin{pmatrix} 0\\ 11/10\\ 11/10 \end{pmatrix} - \begin{pmatrix} 11/4\\ 0\\ 0 \end{pmatrix} = \begin{pmatrix} -11/4\\ 11/10\\ 11/10 \end{pmatrix}\quad \Rightarrow |AH_A| \approx 3,160$$

$$F = \frac12 |BC| \cdot |AH_A| = \frac12 \cdot 3,111 \cdot 3,160 \approx 4,915$$

Comments

Dankeschön sehr gut erklärt echt top !!

Also hat Dieb Dreiecksfläche eine Größe von F= 4,915

Könnten sie mir auch die andere frage die ich gestellt habe so Präzise erklären das wäre echt sehr nett !