Aufgabe Bogenlänge :
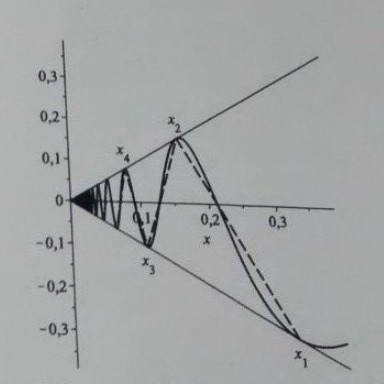
Gegeben sei die abgebildete Funktion
$$ y(x)=\left\{\begin{array}{lll} x \cos \frac{1}{x} & \text { für } & x>0 \\ 0 & \text { für } & x=0 \end{array}\right. $$
a) Berechnen Sie die Ableitung der Funktion und untersuchen sie deren Verhalten im Grenzfall \( x \rightarrow 0 \).
b) Sei \( s(x) \) die Bogenlänge der Kurve bezogen auf den Punkt \( x_{1}=1 / \pi \). Schreiben Sie einen Integralausdruck für \( s(x) \) hin.
c) Beweisen Sie, dass gilt \( s(0)=\infty \), d.h. die Gesamtlänge der Kurve zwischen \( x=x_{1} \) und \( x=0 \) ist unendlich. Anstatt das Integral zu lösen kann für eine Abschätzung ihrer Länge die Kurve wie abgebildet durch eine Zickzacklinie aus geraden Teilstücken angenähert werden.
Hinweis: Die "harmonische Reihe" \( \sum \limits_{n=1}^{\infty} \frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\ldots \) divergiert.