2 Straßen sollen miteinander verbunden werden. Polynom -.-

Question

(1) Zwei Straßen sollen miteinander geeignet verbunden werden. Der Verlauf der ersten Straße entspricht

der Funktion f(x) := x^3  auf dem Intervall [0, 1]. Der Verlauf der zweiten Straße wird auf

dem Intervall [2, 3] durch die Funktion g(x) := 0, 1 (x-3)^2+1, 1 deniert. Wie sieht das Polynom

für das fehlende Stück des Intervalls [1, 2] aus, wenn die Gesamtstraÿe stetig und ohne Knicke sein

soll? Fertigen Sie bitte eine Skizze an.

Answer 1

f(x) = x^3

g(x) = 0.1·(x - 3)^2 + 1.1

p(1) = f(1) = 1

p'(1) = f'(1) = 3

p(2) = g(2) = 1.2

p'(2) = g'(2) = -0.2

Nutze zur Kontrolle

f(x) = 2.4·x^3 - 12.4·x^2 + 20.6·x - 9.6

~plot~ x^3*(x<1);(0.1*(x-3)^2+1.1)*(x>2);(2.4*x^3-12.4*x^2+20.6*x-9.6)*(x>1)*(x<2);[[-1|3|-1|2]] ~plot~

Answer 2

Hallo NFK,

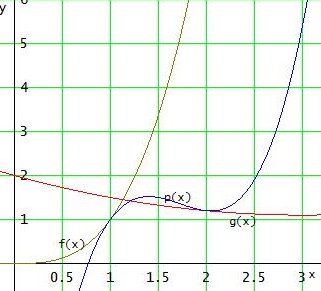
p(x) soll  f(x) = x³  über  [0,1]   und  g(x) =  0,1 (x-3)² +1,1 über [2,3]   im Intervall  [1,2]  knickfrei verbinden.

f '(x) = 3x²  ;   g '(x) =  0,2 · (x-3)  

Bedingungen:

f(1) = p(1)             ⇔     a + b + c + d = 1

g(2) = p(2)            ⇔     8·a + 4·b + 2·c + d = 1,2

f '(1) = p '(1)          ⇔    3·a + 2·b + c = 3  

g '(2) = p '(2)         ⇔    12·a + 4·b + c = - 0,2 

LGS lösen ergibt:

a = 2,4  ;  b = - 12,4  ;  c = 20,6  ;  d = - 9,6

p(x)  =  2,4·x³ - 12,4·x² + 20,6·x - 9,6

Gruß Wolfgang