Hallo Mathefrager,
Ich habe das Stück Pappe mit den Knickkanten eingezeichnet:
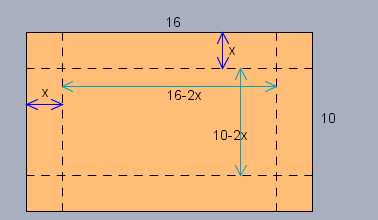
Wenn an allen vier Seiten \(x\)cm weg fallen, so bleibt für die Grundfläche \(G\) der Schachtel noch
$$G=(16-2x)(10-2x)$$
übrig. Das Volumen der Schachtel ist dann
$$V(x)=G \cdot x = (16-2x)(10-2x)x = 4x^3 - 52x^2 +160x$$
Die Funktion für das Volumen in Abhängigkeit von \(x\) sieht so aus (blau):
~plot~ 4x^3-52x^2+160x;[[-1|10|-40|160]];{2|144};12x^2-104x+160 ~plot~
Sinnvoll sind nur Werte für \(x\), die zwischen 0 und 5 liegen. Bei \(x=5\) würde man die Pappe längst in der Mitte knicken und die Grundfläche wäre =0. Man sieht auch im Graphen, dass das Volumen bei \(x=5\) wieder zu 0 wird.
Um das Maximum zu berechnen, leitet man die Funktion für das Volumen nach \(x\) ab und setzt diese zu 0.
$$V'(x_{max})= 12x^2-104x+160 = 0$$
Dies ist die rote Kurve oben im Graphen. Man sieht, dass sie bei \(x=2\) die X-Achse schneidet. Das überprüfen wir per Rechnung:
$$12x^2-104x+160 = 0$$
$$x_{1,2} = \frac{104 \pm \sqrt{104^2 - 4 \cdot 12 \cdot 160}}{2 \cdot 12}=\frac{13}{3} \pm \frac73$$Die Lösung \(x_1=20/3>5\) entfällt, so bleibt nur noch wie erwartet \(x_2=\frac{13}{3} - \frac73=2\). Streng genommen muss man nun noch prüfen, ob die dritte Ableitung an der Stelle \(x=2\) negativ ist.$$V''(x)=24x-104 \quad V''(x=2)=24 \cdot 2 - 104 = -56$$
Ja - das ist der Fall. Folglich liegt bei \(x=2\) ein Maximum vor.
Gruß Werner