Überführen Sie dieses Fünfeck in ein Viereck. Begründen Sie die Flächeninhaltsgleichheit von Viereck und Fünfeck.

Question

Gegeben ist das Fünfeck ABCDE mit den Eckpunkten А=(0, 5), В=(4, 3), С=(8, 6), D=(8, 8), E=(4, 8). Überführen Sie dieses Fünfeck in ein flächeninhaltsgleiches Viereck und beschreiben Sie die Konstruktionsschritte. Begründen Sie die Flächeninhaltsgleichheit von Viereck und Fünfeck.

Könnt ihr mir bitte helfen?

Answer 1

Hallo Sabrina,

die Fläche \(F\) eines Dreiecks berechnet sich aus der Hälfte von Grundseite \(c\) mal Höhe \(h\)

$$F = \frac12 c\cdot h$$

D.h. zwei Dreiecke mit einer gleichen Seite und der dazugehörigen gleichen Höhe haben den gleichen Flächeninhalt.

 

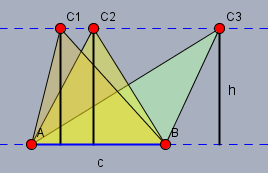
so wie die drei oben gezeigten Dreiecke. Bei ihnen wurde nur der Punkt \(C\) parallel zur Grundseite \(c\) verschoben. Genau das gleiche kann man nun mit Teildreiecken des Fünfecks machen.

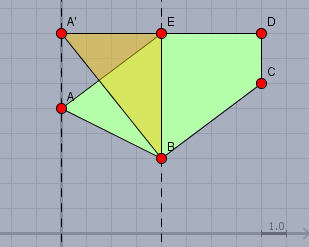
Betrachte das Teildreieck \(BEA\). Ich verschiebe den Punkt \(A\) parallel zur Seite \(BE\) nach \(A'\). Dadurch ändert sich der Flächeninhalt von \(BEA'\) gegenüber \(BEA\) nicht, da die Seite \(BE\) und die Höhe von \(A\) bzw,. \(A'\) über der Seite unverändert bleibt. Der Effekt führt aber dazu, dass die Ecke bei \(E\) entfernt wird.

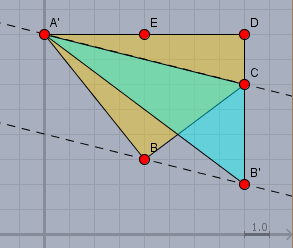
Beim verbleibenden Viereck verschiebe ich nun die Ecke \(B\) parallel zur Grundseite des Dreiecks \(CA'B\) - also parallel zu \(CA'\) nach \(B'\). Da die Gerade durch \(A'C\) eine Steigung von \(-2 \div 8=-1 \div 4\) hat, ist dies sehr einfach. Ich addiere zur X-Koordinate von \(B\) die \(4\) und ziehe von der Y-Koordinate die \(1\) ab und aus \(B=(4;3)\) wird \(B'=(8;2)\). Nun bleibt das rechtwinkliges Dreieck \(A'B'D\) übrig. Und es war Absicht, dass ich die Ecke, die schon einen rechten Winkel hat (die bei \(D\)) stehen gelassen habe!

 

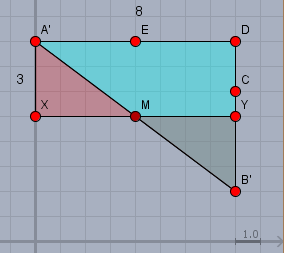
Ein rechtwinkliges Dreieck lässt sich nun leicht in ein flächengleiches Rechteck verwandeln. Der Mittelpunkt der Hypotenuse \(A'B'\) sei \(M\) . Dann ziehe man eine Parallele zu einer der Katheten (hier \(A'D\)) durch \(M\) die von dem Dreieck \(A'B'D\) das kleinere Dreieck \(MB'Y\) abschneidet. Und dies klappt man in die Lücke von \(A'MX\). \(X\) und \(Y\) stehen punktsymmetrisch zu \(M\). Das Rechteck \(XYDA'\) hat die gleiche Fläche wie das ursprüngliche Fünfeck. Nämlich \(F=3\cdot8=24\).

Gruß Werner

Comments

Das ist sehr beeindruckend, die Aufgabe fordert aber doch wesentlich weniger: Nimm drei benachbarte Punkte, zum Beispiel A, B und E wie in deinem zweiten Bild, und schere das Dreieck ABE durch Verschiebung des Punktes A parallel zur Geraden BE so, dass A' auf der Geraden BC oder der Geraden DE liegt. Es entsteht das Viereck A'CDE bzw. das Viereck A'BCD. Beide Vierecke sind flächengleich zum ursprünglichen Fünfeck ABCDE.

---

Du schriebst: "Nimm drei benachbarte Punkte, zum Beispiel A, B und E wie in deinem zweiten Bild, und schere das Dreieck ABE durch Verschiebung des Punktes A parallel zur Geraden BE so, dass A' auf ... der Geraden DE liegt."

Genau das habe ich doch oben gemacht - oder wo siehst Du den Unterschied!??

Gruß Werner

---

Eigentlich wollte ich nur darauf hinweisen, dass dies bereits völlig ausgereicht hätte...

---

Jetzt verstehe ich Dich erst! In der Aufgabe steht 'Viereck' und nicht 'Rechteck'. Sag das doch gleich! Das kommt von den Scheuklappen, mit denen man durch die Gegend läuft. Könnte aber gut sein, dass Rechteck gemeint ist - oder? ;-)

Gruß Werner

---

In der Aufgabe steht 'Viereck' und nicht 'Rechteck'. Sag das doch gleich!

Tja, das hätte ich wohl machen können, aber beim Durchlesen war mir überhaupt nicht klar, welches Ziel du da verfolgst.

Könnte aber gut sein, dass Rechteck gemeint ist - oder? ;-)

Was der Aufgabensteller meinte, weiß ich auch nicht, die "Rechteck"-Idee kam mir aber nicht in den Sinn, zumal in der Frage der Begriff "Rechteck" gar nicht, der Begriff "Viereck" jedoch zweimal vorkommt.

---

Schade, dass sich Sabrina zu dem Thema nicht äußert ...

Answer 2

Das Trapez BCDE wird in ein Rechteck verwandelt (Schnitt durch die Mitte von BC parallel zu ED).Das Dreieck ABE wird auf ganz ähliche Weise in ein Rechteck umgewandelt (eine Seite des Rechtecks ist die halbe Höhe auf BE, eine Seite ist BE).Dieses Rechteck muss noch in eines verwandelt werden, dass in einer Seitenlänge mit den ersten übereinstimmt (googeln unter "Flächenanlegen").

Answer 3

AE || BC und AB || CE. Also ist das Viereck ABCE ein Parallelogram. Unterschied zum Fünfeck ist das Dreieck CDE. Dessen Flächeninhalt ist 1/2 · CE · DH, wobei H der Lotfusspunkt von D auf die Gerade durch E und C ist.

1. Konstruiere den Punkt H.
2. Konstruiere den Mittelpunkt M der Strecke DH.
3. Konstruiere die Parallele p zu EC durch M.
4. Der Schnittpunkt von p und der Geraden durch B und C sei C'.
5. Der Schnittpunkt von p und der Geraden durch A und E sei E'.

Das Viereck ABC'E' hat den gleichen Flächeninhalt wie das Fünfeck ABCDE.