Senkrechte Tangente bestimmen bei Schwingungen

Question

Hallo :)

Ich habe eine Aufgabe bei der ich absolut keine Ahnung habe was ich machen muss um sie zu lösen...

Wäre sehr dankbar, wenn mir Jemand weiter helfen könnte :)

Answer 1

Hallo Unicorn,

Mache Dir ein Bild von der Lissajous-Figur - die sieht so aus (\(a=1\)):

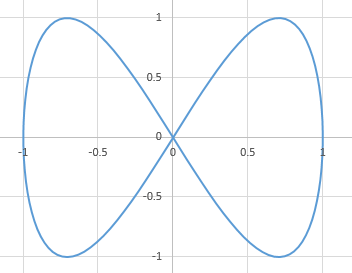
Senkrechte Tangenten scheint es in den Punkten \((1;0)\) und \((-1;0)\) zu geben. Rein formal liegt eine senkrechte Tangente vor, wenn 

$$\frac{\partial x}{ \partial y} = 0$$

ist. Bzw.

$$\frac{\partial x}{ \partial y}  = \frac{\partial x}{ \partial t} \cdot \frac{\partial t}{ \partial y} = \frac{\partial x}{ \partial t} \div \frac{\partial y}{ \partial t}= 0$$

D.h. die Ableitung von \(x\) nach \(t\) muss \(=0\) sein und die von \(y\) nicht. Es ist

$$\frac{\partial x}{ \partial t} = \dot x = a \cos t$$

$$\frac{\partial y}{ \partial t} = \dot y = 2a \cos 2t$$

In den Punkten \(t_1=\frac12 \pi\) und \(t_2=\frac32 \pi\) ist \(\dot x(t_{1,2})=0\) und \(y_{1,2} \ne 0\).

Für eine waagerechte Tangente muss gelten

$$\frac{\partial y}{ \partial x}  = \frac{\partial y}{ \partial t} \cdot \frac{\partial t}{ \partial x} = \frac{\partial y}{ \partial t} \div \frac{\partial x}{ \partial t}= 0$$

heißt die Ableitung nach \(y\) muss \(=0\) sein und die Ableitung von \(x\) nach \(t\) darf nicht \(=0\) sein. Und \(\dot x(t_{3..6}) \ne 0 \) und \(\dot y(t_{3..6})= 0\) ist der Fall für \(t_3 = \frac14 \pi\), \(t_4=\frac34 \pi\), \(t_5=\frac54 \pi\) und \(t_6=\frac74 \pi\).

Gruß Werner

Comments

Vielen Dank :)

Aber ich verstehe nicht ganz wie man auf diese Bedingung kommt:

 

Was ist die Aussage dahinter?

---

Also die Steigung einer Funktion ist Dir sicher ein Begriff - es ist

$$y'= \frac{\partial y}{ \partial x} = f'(x)$$

Wenn der Wert für die Steigung in einem bestimmten Punkt \(=0\) ist, verläuft die Funktion in diesem Punkt waagerecht. Wird der Wert größer, so wächst auch die Steigung der Funktion. Um einen senkrechten Funktionsverlauf zu erreichen, müsste der Wert gegen unendlich \(\infty\) gehen. Oder (!) - wenn man den reziproken Wert bestimmt - es müsste \(\partial x/\partial y = 0\) sein.

D.h. die Bedingung für eine senkrechte Steigung in einem XY-Koordinatensystem ist

$$ \frac{\partial y}{ \partial x}= \infty \quad \Rightarrow \frac{\partial x}{ \partial y} = 0 $$

da aber keine Funktion \(y=f(x)\) sondern 'nur' zwei Funktionen \(x=x(t)\) und \(y=y(t)\) gegeben sind, erweitere ich obigen Bruch mit \(\partial t\):

$$\frac{\partial x}{ \partial y} = \frac{\partial x \cdot \partial t}{ \partial y \cdot \partial t} = \frac{\partial x}{\partial t} \cdot \frac{\partial t}{\partial y }$$

... und die Ableitungen nach \(t\) lassen sich berechnen.

Falls etwas nicht klar ist, bitte nochmal nachfragen.

Gruß Werner