Senkrechte Tangente bestimmen bei Schwingungen

Question

Hallo :)

Ich habe eine Aufgabe bei der ich absolut keine Ahnung habe was ich machen muss um sie zu lösen...

Wäre sehr dankbar, wenn mir Jemand weiter helfen könnte :)

Answer 1

Hallo Unicorn,

Mache Dir ein Bild von der Lissajous-Figur - die sieht so aus ($a=1$):

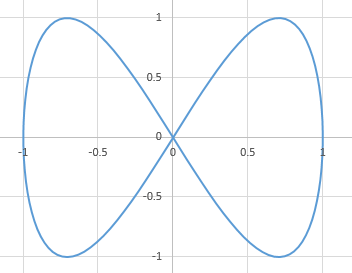
Senkrechte Tangenten scheint es in den Punkten $(1;0)$ und $(-1;0)$ zu geben. Rein formal liegt eine senkrechte Tangente vor, wenn

$$\frac{\partial x}{ \partial y} = 0$$

ist. Bzw.

$$\frac{\partial x}{ \partial y} = \frac{\partial x}{ \partial t} \cdot \frac{\partial t}{ \partial y} = \frac{\partial x}{ \partial t} \div \frac{\partial y}{ \partial t}= 0$$

D.h. die Ableitung von $x$ nach $t$ muss $=0$ sein und die von $y$ nicht. Es ist

$$\frac{\partial x}{ \partial t} = \dot x = a \cos t$$

$$\frac{\partial y}{ \partial t} = \dot y = 2a \cos 2t$$

In den Punkten $t_1=\frac12 \pi$ und $t_2=\frac32 \pi$ ist $\dot x(t_{1,2})=0$ und $y_{1,2} \ne 0$.

Für eine waagerechte Tangente muss gelten

$$\frac{\partial y}{ \partial x} = \frac{\partial y}{ \partial t} \cdot \frac{\partial t}{ \partial x} = \frac{\partial y}{ \partial t} \div \frac{\partial x}{ \partial t}= 0$$

heißt die Ableitung nach $y$ muss $=0$ sein und die Ableitung von $x$ nach $t$ darf nicht $=0$ sein. Und $\dot x(t_{3..6}) \ne 0$ und $\dot y(t_{3..6})= 0$ ist der Fall für $t_3 = \frac14 \pi$, $t_4=\frac34 \pi$, $t_5=\frac54 \pi$ und $t_6=\frac74 \pi$.

Gruß Werner

Comments

Vielen Dank :)

Aber ich verstehe nicht ganz wie man auf diese Bedingung kommt:

 

Was ist die Aussage dahinter?

---

Also die Steigung einer Funktion ist Dir sicher ein Begriff - es ist

$$y'= \frac{\partial y}{ \partial x} = f'(x)$$

Wenn der Wert für die Steigung in einem bestimmten Punkt $=0$ ist, verläuft die Funktion in diesem Punkt waagerecht. Wird der Wert größer, so wächst auch die Steigung der Funktion. Um einen senkrechten Funktionsverlauf zu erreichen, müsste der Wert gegen unendlich $\infty$ gehen. Oder (!) - wenn man den reziproken Wert bestimmt - es müsste $\partial x/\partial y = 0$ sein.

D.h. die Bedingung für eine senkrechte Steigung in einem XY-Koordinatensystem ist

$$\frac{\partial y}{ \partial x}= \infty \quad \Rightarrow \frac{\partial x}{ \partial y} = 0$$

da aber keine Funktion $y=f(x)$ sondern 'nur' zwei Funktionen $x=x(t)$ und $y=y(t)$ gegeben sind, erweitere ich obigen Bruch mit $\partial t$:

$$\frac{\partial x}{ \partial y} = \frac{\partial x \cdot \partial t}{ \partial y \cdot \partial t} = \frac{\partial x}{\partial t} \cdot \frac{\partial t}{\partial y }$$

... und die Ableitungen nach $t$ lassen sich berechnen.

Falls etwas nicht klar ist, bitte nochmal nachfragen.

Gruß Werner