Hallo Janet! :-)
Wir bezeichnen den Weg mit w und erhalten mit dem Satz des Pythagoras:
w^2 = x^2 + (y - 1/2)^2
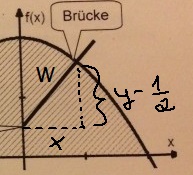
Wir ziehen die Wurzel und bekommen für den Weg
w = √(x^2 + (y - 1/2)^2)
Damit w nur von x abhängt, ersetzen wir y durch den Funktionsterm -1/2x^2 + 2
w(x) = √(x^2 + (-1/2x^2 + 2 - 1/2)^2) wir lösen die innere Klammer auf und fassen so weit wie möglich zusammen und bekommen
nach Ausklammern von 1/4
w(x) = √(1/4 (x^4 - 2 x^2 + 9)) = 1/2√(x^4 - 2 x^2 + 9)
Der Weg w(x) = 1/2√(x^4 - 2 x^2 + 9) vom Automaten zur Brücke soll minimal sein.
Ein Minimum liegt vor, wenn die erste Ableitung von w(x) Null wird, wenn also w'(x) = 0 gilt.
Wir berechnen erstmal die erste Ableitung von w(x) mit der Kettenregel:
w(x) = 1/2(x^4 - 2 x^2 + 9)^{1/2}
Innere Ableitung: 4x^3 - 4x = 4(x^3-x)
Äußere Ableitung: 1/4*(x^4 - 2 x^2 + 9)^{-1/2}
w'(x) = Innere Ableitung mal äußere Ableitung
w'(x) = 4(x^3-x)*1/4*(x^4 - 2x^2 + 9)^{-1/2}
w'(x) = (x^3-x) / (x^4 - 2x^2 + 9)^{1/2}
w'(x) = (x^3 - x)/ √(x^4 - 2x^2 + 9)
Die erste Ableitung wird Null, wenn der Zähler Null wird.
x^3 - x = 0
Wir klammern x aus
x(x^2 - 1) = 0 und wenden den Satz vom Nullprodukt an, der uns die Lösungen
x1=0, x2= √1, x3 = -√1 liefert.
Für uns kommt hier nur die Lösung x = √1 = 1 in Frage und wir
erhalten die Optimale Position der Brücke P(1|f(1)) =
P(1 | 1,5)
Grüße