Hallo SomO,
was verstehst Du an der Aufgabe nicht? Dies ist ein weißes Quadrat ...

... mit der Kantenlänge \(2\text{dm}\). Und da wird symmetrisch ein blaues Kreuz eingezeichnet:
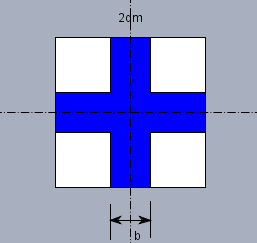
Einige Symmetrielinien habe ich mit Strich-Punkt eingezeichnet. Jeder "Arm" des Kreuzes hat die Breite \(b\). Diese \(b\) ist die gesuchte Breite des Kreuzes. Ein kleines weißes Quadrat hat die Kantenlänge \(s_Q\) von
$$s_Q = \frac12 \left( 2 \text{dm} - b\right) = 1 \text{dm} - \frac12 b$$
Demnach hat es die Fläche \(F_Q\)
$$F_Q = s_Q^2 = \left( 1 \text{dm} - \frac12 b\right)^2$$
Und die Forderung ist nun dass die blaue Fläche genauso groß sein soll wie die weiße - also beide die Hälfte des Quadrats. Also müssen vier Quadrate die halbe Fläche des Quadrats ergeben:
$$4 F_Q = \frac12 (2 \text{dm})^2 = 2 \text{dm}^2$$
Einsetzten der \(F_Q\) von oben gibt
$$4 \left( 1 \text{dm} - \frac12 b\right)^2 = 2 \text{dm}^2$$
das ganze durch 4 teilen und die Wurzel ziehen:
$$1 \text{dm} - \frac12 b = \sqrt{\frac12} \text{dm}$$
\(\frac12 b\) addieren und \(\sqrt{\frac12} \text{dm}\) abziehen
$$1 \text{dm} - \sqrt{\frac12} \text{dm}=\frac12 b $$
Jetzt noch mal 2, die Seiten tauschen und den Wert berechnen
$$b=2 \left( 1 -\sqrt{\frac12} \right) \text{dm} \approx 0,59\text{dm}$$
Gruß Werner