Ich glaube, dass ein solcher Körper nicht existieren kann.
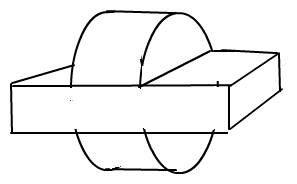
Begründung: Der Körper müsste etwa so aussehen, wie auf der unten abgebildeten "Zeichnung": Ein quadratischer Zylinder, dessen Grundfläche eine Seitenlänge von 6 cm hat und der 2 cm hoch ist, wird mittig von einem Kreiszylinder durchdrungen, dessen kreisförmige Grundfläche einen Durchmesser von 6 cm hat und dessen Höhe ebenfalls 2 cm beträgt.
Das Problem ist jedoch: Wenn man von der Seite auf diesen Körper schauend einen Kreis sehen soll, dann muss der abgebildete Kreiszylinder vollständig sein, er darf also vorne und hinten nicht abgeplattet sein. Das aber müsste er sein, damit man von oben betrachtet ein Quadrat sieht, welches an keiner Stelle "ausgebuchtet" ist.
Verringert man den Radius des Kreiszylinders so, dass er die begrenzenden vorderen und hinteren Seitenflächen des quadratischen Zylinders von innen gerade berührt, dann sieht man, wenn man den Körper von der Seite anschaut, einen Kreis mit eckigen "Ausbuchtungen", die von der Seitenansicht des quadratischen Zylinders herrühren.
Ein Körper der abgebildeten Form, der in der Seitenansicht wie ein korrekter Kreis und in der Draufsicht gleichzeitig wie ein korrektes Quadrat aussieht, ist meines Erachtens nicht möglich. Einen anders geformten Körper, der die genannten Bedingungen erfüllt, kann ich mir hingegen gerade nicht so recht vorstellen. Vielleicht kann das ja jemand anderes (und kann dazu auch eine grobe Skizze liefern) ... ?