Das Kalenderjahr und die Dauer der einzelnen Tage

Question

mit folgender Funktion lässt sich die Tagesdauer d (Zeitspanne zwischen Sonnenaufgang und Sonnenuntergang) in Abhängigkeit von der Zeit t beschreiben.

d(t) =4,25*cos(2*π/365(t-172))+12,25

1. Bestimmen Sie die Dauer des längsten Tages des Jahres.

2. Berechnen Sie, an welchen Tagen des Jahres die Tagesdauer ungefähr 15 Stunden beträgt. 

3. Geben Sie das Monotonieverhalten der Funktion in Intervallschreibweise an und interpretieren Sie es im Sachzusammenhang. 

4. Zeigen Sie, dass zu Frühlingsbeginn und Herbstbeginn Tag und Nacht gleich lang sind. 

Danke für die Hilfe!! 

Answer 1

Hi,

wir fangen mal langsam mit der a) an:
d(t) gibt uns die Dauer des Tages t an. Wir sollen nun den Tag t bestimmen für den d(t) am größten wird. In was für einem Punkt wird denn der größte Wert einer Funktion angenommen?

Answer 2

d(t) =4,25*cos(2*π/365(t-172))+12,25

1. Bestimmen Sie die Dauer des längsten Tages des Jahres.

Vorgehen : 1.Ableitung bilden, zu nuil setzen
und t berechnen

Es bedeuten ( eingekreiste rote Zahlen )

0 : die Ausgangsfunktion

[ cos ( term ) ] ´ = - sin ( term ) * ( term ´ )
term = 2 * PI * ( t - 172 ) / 365
1 : term ´

2 : d ´ ( t )

3 : d ´( t ) etwas zusammengefasster

4.) d ´( t ) = 0 setzen und den Satz vom Nullprodukt
anwenden

5.) sin ( term ) = 0
d.h. term = 0 oder Pi
term =  0

2 * PI / 365 * ( t - 172 ) = 0
Satz vom Nullprodukt anwenden
( t - 172 ) = 0
t = 172



Das war es zunächst. Bei Bedarf nachfragen oder
sagen ob es weiter gehen soll

Answer 3

Hallo Queenie,

1)

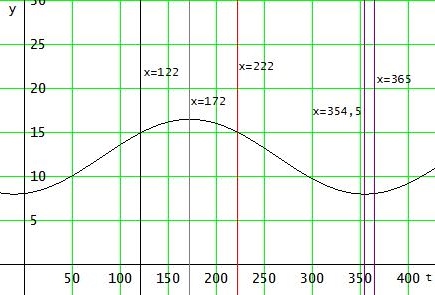
d(t) = 4.25·COS(2·π/365·(t - 172)) + 12.25  soll maximal sein.

Wegen  -1 ≤ cos(x) ≤ 1 ist das genau dann der Fall, wenn der cos-Term den Wert 1 hat:

2·π/365·(t - 172) = 0     →  t = 172

2) 

D = [0 ; 365]

4.25·COS(2·π/365·(t - 172)) + 12.25 = 15  

COS(2·π/365·(t - 172)) ≈ 0,64706    | arccos

  t ≈  222.37 ≈  222    

Ein weiterer Wert für t ergibt sich aus  172 + (172 - 222.37)  ≈  121.63  ≈ 122 

denn die beiden t-Werte mit d(t) = 15 sind von der Maximalstelle x =172 gleich weit entfernt.

3)   

   Minimalstelle =  ( Maximalstelle  x=172)  +   halbe Periode   =  172 + 365/2 = 354,5

      [ Die Periode von cos(bx+c) ist bekanntlich 2π/b,  hier  = 2π / ( 2π/365) = 365 ]  

   Mit D = [0 ; 365]

   d streng monoton steigend  in [ 0 ; 172]  ∪ [354,5 ; 365]  

   streng monoton fallend in  [172 ; 354,5]  

> interpretieren Sie es im Sachzusammenhang (Jahreszeiten)  dürfte klar sein

4)

  4.25·COS(2·π/365·(t - 172)) + 12.25 = 12   (d(t) = 12 ↔ Tag = Nacht )

     t ≈ 77  oder    t ≈ 267     (wie oben bei 2)  ... = 15)

  Wenn man die Tage nachzählt, kommt das mit den Jahreszeiten etwa hin.

Gruß Wolfgang