Lösen einer trigonometrischen Gleichung sin^{2} x = 55/36 -sinx

Question

nabend,

komme hier nicht weiter:

sin^2 x = 55/36 -sinx

will die Lösungen für das Intervall [0,π] berechnen.

danke!

Answer 1

Substituiere \(\sin x = z\). Dann erhältst Du

$$z^2 = \frac{55}{36} - z$$Umstellen ergibt eine klassische quadratische Gleichung

$$z^2 + z - \frac{55}{36} = 0$$mit den Lösungen

$$z_1 = \frac{5}{6}; \quad z_2 = \frac{-11}{6}$$

Die zweite Lösung scheidet aus, da \(|\sin x| \le 1\) sein muss. Bleibt noch \(z_1\) über. Das schaut man sich im Einheitskreis an, damit man alle Lösungen erwischt:

 

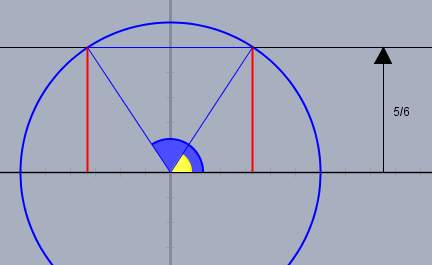
Die \(5/6\)-Linie schneidet den Einheitskreis 2mal. Es sind zwei Winkel als Lösung möglich, der blaue und der gelbe. Der Taschenrechner liefert:

$$x_1 = \arcsin \frac{5}{6} \approx 0,9851 \approx 56,44°$$das wäre der gelbe Winkel \(x_1\) und der blaue \(x_2\) muss demnach

$$x_2 = \pi - x_1 \approx 2,1565 \approx 123,56°$$ betragen

Gruß Werner

Answer 2

könnte es so funktionieren?

$$sin^{2} x = 55/36 - sinx  |  - 55/36 + sinx $$$$sin^{2} x + sinx - 55/36 = 0 \quad|\quad Substitution: sin x = z $$$$z^{2} + z - 55/36 = 0  \quad|\quad mit\quad pq-Formel \quad auflösen$$