Normalapproximation Wahrscheinlichkeit

Question

Hi Leute bräuchte bei folgender Aufgabe Hilfe :

Es bildet sich die Initiative S.C.H.N.A.T.Z. mit der Forderung, dass Eintrittskarten für die Quidditch-Weltmeisterschaft nicht mehr zufällig verteilt werden, sondern jeder Studierende garantiert eine Karte bekommt. Die 35000 Studierenden entscheiden nun in einer Urabstimmung darüber, ob diese Regelung eingeführt werden soll oder nicht. 350 Studierende wissen bereits, dass dem Vorschlag zustimmen werden. Die restlichen Studierenden sind unentschlossen und treffen ihre Entscheidung unabhängig voneinander mit einem fairen Münzwurf. Berechnen Sie mittels einer Normalapproximation näherungsweise die Wahrscheinlichkeit, dass die Forderung von S.C.H.N.A.T.Z. eine Mehrheit findet.

Hier auch nochmal was wir unter einer Normalapproximation verstehen :

Liebe Grüße 

Kevin

Comments

Also habe mich an einer ähnlichen Aufgabe im Internet orientiert und hab nun :


n = 34650 ;  p = 0,5 

P(X ≥ 17151)      

Doch wie berechne ich es nun weiter ? und stimmt es so weit ?

Answer 1

Hallo kevsch1, ich habe die Aufgabe jetzt erst mal ohne Approximation, sondern „exakt“ gelöst.  Hierzu habe ich einen Taschenrechner mit Binomialverteilung benutzt. 

Siehe mein Bild. 

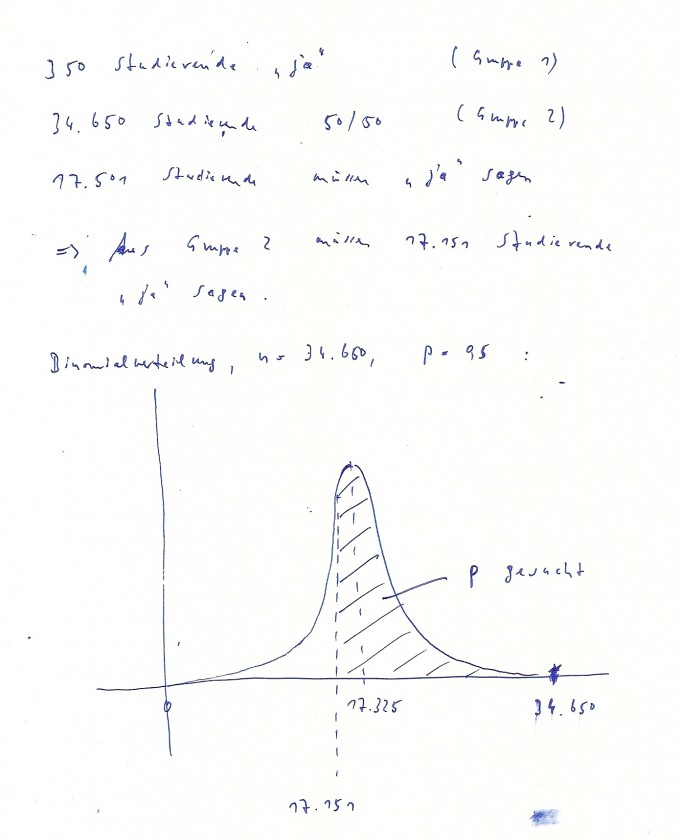
Die weitere Rechnung:  P(17.151 <= x <= 34.650) = Taschenrechner = 1 – binomcdf(n, p, 17.150) = 1 – binomcdf(34.650, 0,5, 17.150) = 96,96 %.

Die gesuchte Wahrscheinlichkeit ist 96,96 %.