Extremwertaufgabe: Pyramide mit quadratischer Grundfläche (maximales Volumen)

Question

ich komme leider nicht weiter ...
Eine Pyramide mit quadratischer Grundfläche (a=8cm; h=12cm) ist eine quadratische Säule mit maximalem Volumen einzuberechnen.
Ich habe mal angefangen und bekam das raus .... weiter komm ich nicht :/
Extremalbedingung : V(b,c)= (2*b)²   * c

Nebenbedingung : ?

Zielfunktion : ?
Danke schon mal  :)

Answer 1

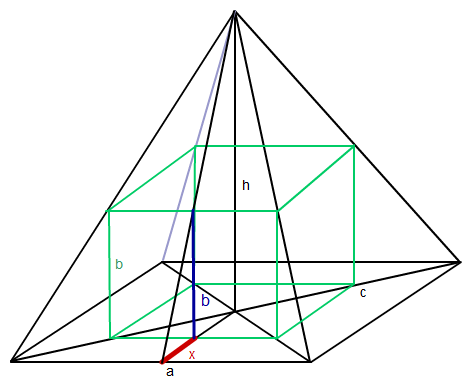
Skizze: Quadratische Pyramide mit einbeschriebener quadratischer Säule (a = 8 cm, h = 12 cm).

b - Höhe der Säule
c - Seitenlänge der Grundfläche der Säule

h = 12 cm; - Höhe der Pyramide
a = 8cm; - Seitenlänge der Grundfläche der Pyramide

 

Der Zusammenhang zwischen b und x ist die Steigung m. m = 2*h/a = 3 (vgl. Geradengleichung).

b = m*x = 2*h/a*x = 3*x;    0 ≤ x ≤ a/2;

 

Die Seitenlänge der Grundfläche der Säule lässt sich ebenfalls in Abhängigkeit von x darstellen:

c = a -2x = 8 -2x;

 

Damit beträgt das Volumen der Säule:

V(x) = b*c^2 = 2*h/a*x  *(a-2x)^2 = 3x *(8 -2x)^2;
 

V(x) = 12x^3 -96x^2 +192x;

V'(x) = 36x^2 -192x +192;

 

Die Ableitung liefert:

V'(x) = 0; x₁ = 4; x₂ = 4/3;

 

Eigentlich müsste man jetzt die Extrempunkte untersuchen. Das spare ich mir. (Eine Anmerkung: Bei den Intervallgrenzen liegen ebenfalls Extrema. Da jedoch das Volumen bei x = 0 oder x = 4 Null wird, können das nicht die gesuchten Stellen sein.)

x₁ = 4 scheidet aus. Damit bleibt x₂ = 4/3.

Das gesuchte Volumen beträgt also V(x=4/3) = 3*4/3  *(8-2*4/3)^2 = 1024/9 ≈ 114.

(Die Einheiten habe ich weggelassen um etwas Schreibaufwand zu sparen. Das ist hier unproblematisch da alle Längen in cm, alle Flächen in cm^2 und alle Volumina in cm^3 angegeben sind.)

 

Falls etwas unklar ist, Du einen Fehler in meinen Überlegungen entdeckst --> Kommentar.

 

lg JR

Comments

Vielen Dank :)

alles ist sehr verständlich :)

---

Bitte sehr. Freut mich, wenn es Dir weiterhilft.