Exponentiagleichung lösen: 90 - 80e^{-0.05 t} = 10e^{0.038 t}

Question

Hallo , also ich müss diese Gleichung hier lösen, doch ich habe keinen blassen schimmer wie ich das machen soll, Dankeschön

Comments

Benutze eine Tachenrechner, der so etwas lösen kann...

---

Ja aber wir geht das von Hand? Und ich habe keine Ahnung, wie man das in den Taschenrechner eingibt , welche Funktion man dazu verwendet...

---

Hast du diese Aufgabe selber erfunden? 

Wenn nicht, kannst du es mit einem dir bekannten numerischen Verfahren versuchen. 

---

Vom Duplikat:

Titel: Schnittpunkte der beiden Graphen ermitteln

Stichworte: schnittpunkt,graphen,berechnen

Ich muss die Schnittpunkte der beiden Graphen ermitteln, und am Anfang ist das noch richtig, also mit dem gleichsetzen der Funktionen, doch mein Ergebnis ist falsch, weil es t1=0 und t2=56,39 lauten muss, Wäre sehr toll, wenn ihr dort für mich weiterrechnen könntet, ab wo ich den Fehler gemacht habe, stehe nämlich aufm Schlauch :/

---

Mich wundert das du eine Aufgabe
rechnen sollst die das Newton-Verfahren
zur Lösung benötigt.
Habt ihr das im Unterricht denn schon
gehabt ?
Oder wo hast du die Aufgabe her ?

---

Ich habe sie aus dem Abi-Starkheft, und das Newtonverfahren habe ich mir quasi selbst beigebracht,  aber wenn man erst nach 147 auf ein näherungsweise richtiges Ergebnis kommt, wäre es doch auch mit dem Newtomverfahren zu komplex oder?

---

So sehe ich das auch! 

---

@Wolfgang, danke dir :-), hier ist noch die Aufgabe dazu, es handelt sich um die 1.4, aber die Prüfung lasse ich dann mal aus, man kann es auch glaube ich dann mit einem speziellen Taschenrechner berechnen, den ich nicht besitze :D

---

Nikiii, du solltest immer die Originalfrage
als Foto einstellen.

ich vermute einmal das auf der Abbildung 1
( wurde von dir nicht eingestellt ) der Wert
von t ablesbar ist.
Damit kann der Faktor a leicht berechnet
werden.

Das Newton-Verfahren ist nicht notwendig.

Stell einmal die Abbildung ein.

---

Hier kommt die Abbildung Nr.1

---

Bitte noch die Tabelle in Material 2
einstellen die in 1.2 angeführt wurde.

---

Oh stimmt, tut mir leid hier ist noch der Rest: 

---

Die Gleichung die du oben eingestellt hast
f ( t ) = g ( t ) ist völlig richtig.

Die Gleichung läßt sich algebraisch nicht
lösen.

Die Gleichung bringt als Belohnung
2 Punkte.

Ich denke die Lösung soll durch bloßes
Ablesen aus der Graphik angegeben werden.

Andere Lösungen hätten wesentlich mehr
als 2 Punkte verdient.

Wenn du willst können wir die anderen
Teilaufgaben  auch durchgehen.

---

Nikkiii,

ich habe den Verdacht das du hier Aufgaben
einstellst die zur Abiturprüfung mit CAS-Rechner
-Unterstützung gedacht sind.

Schau bitte einmal in den Hinweisen in deinem
Buch vom Starkverlag nach ob dies zutrifft.

Diese Vermutung habe ich auch bei deiner
letzten Anfrage " Wie löse ich diese langen
Gleichungen " schon gehabt.

---

"GTR/CAS" steht doch bereits im Titel des Aufgabenblattes!

Answer 1

Hallo Niki,

90 - 80·e^{-0,05 t}  = 10·e^{0,038 t}      

wegen e⁰ = 1  sieht man sofort die Lösung  t₁ = 0

Eine zweite Lösung  kannst man mit dem Newtonverfahren (vgl. unten #) ermitteln:

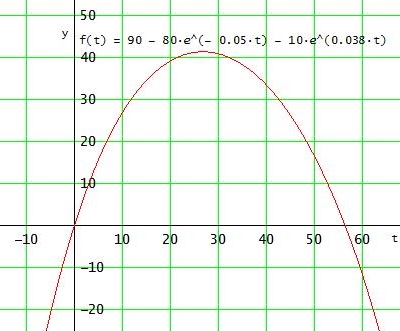
f(t) = 90 - 80·e^{-0,05 t}  - 10·e^{0,038 t}      , gesucht sind die Nullstellen von f     

Aber selbst mit dem guten Startwert x=50 muss man hier ungewöhnlich lang rechnen:

Ich - genauer mein Excelprogrämmchen - erhalte  t₂ ≈ 56,388

( auf diese Stellenzahl nach 204 Rechenschritten gesichert :-) )

Die Ableitung  f '(t) = 4·e^{- t/20} - 19/50 ·e^{19·t/500} 

hat nur eine Nullstelle t = - 125·LN(19/200)/11  ≈  26,749 

Weitere Lösungen der Ausgangsgleichung kann es deshalb nicht geben.

-----------

# Newtonverfahren: 

Berechnen der Nullstellen von f(x)  (f muss differenzierbar sein)
Ausgehend von einem (möglichst guten) Startwert, den man z.B zwischen zwei x-Werten findet, deren Funktionswerte verschiedenes Vorzeichen haben, findet man - auch mit einem einfachen Taschenrechner -  immer bessere Werte mit der Formel
x_neu =  x_alt - f(x_alt) / f ' (x_alt)
Du weißt allerdings i.A. nicht, ob du alle NS gefunden hast.
(vgl. oben die Argumentation mit den Extremstellen) 

Gruß Wolfgang

Answer 2

Hallo Niki,

man kann auf die Differenz rechts nicht einfach den ln anwenden.

Die Gleichung ist (abgesehen von der Lösung t₁ = 0 ) wohl nur mit einem Näherungsverfahren lösbar.

Mit dem Newtonverfahren erhält man z.B. mit dem guten Startwert  t = 50 erst nach 147 Schritten die zweite Lösung  t ≈  56,39  als Lösung der Gleichung  10·e^0.038·t - 90 + 80·e^{- 0.05·t} = 0

https://de.wikipedia.org/wiki/Newton-Verfahren

Gruß Wolfgang

Comments

Wie weiß ich, dass ich dort keinen ln anwenden kann? Du meintest die Differenz? Ist unter Differenz 90-80e^.....   gemeint? Also die Gleichung rechts? Und kann man es nicht noch anders lösen? Vielen Dank schon mal!

---

90  -  10·e^-0,05t  ist eine Differenz.

Deshalb lässt sich  ln (90  -  10·e^-0,05t ) nicht vereinfachen.

Lgarithmensätze:

ln(a * b) = ln(a) + ln(b)

ln(a/b) = ln(a) - ln(b) 

ln(a^b) = b * ln(a)  

Da passt keiner! 

---

Danke, Danke, ! Also ich habe eben gemerkt, dass es wieder eine CAS Aufgabe ist. Aber mit CAS haben wir noch nie gerechnet. Daher kann es doch schon sein, dass sowas im Abi nicht vorkommt..

---

> dass sowas im Abi nicht vorkommt..

Da bin ich ziemlich sicher! 

Habe dir die Frage übrigens unter 

https://www.mathelounge.de/508140/exponentiagleichung-losen-90-80e-0-05-t-10e-0-038-t

schon ausführlicher beantwortet : - )

Da waren nur die Seiten der Gleichung vertauscht.

---

Supi, da bin ich mal erleichtert :D

---

Opsalla! Das habe ich schon wieder total vergessen, dass ich schon mal so was reingestellt habe, danke!:D

---

Du findest deine bisherigen Fragen übrigens hier https://www.mathelounge.de/user/Nikiiiii/questions Schau sie als Repetition mal durch. Vielleicht kannst du dann noch die eine oder andere "beste Antwort" auszeichnen. 

---

@Nikki

wäre schön, wenn du die "Beste Antwort" bei 

https://www.mathelounge.de/508140/exponentiagleichung-losen-90-80e-0-05-t-10e-0-038-t

geben würdest.

Diese Frage wird nämlich als Duplikat gelöscht!

(Die Löschung war noch nicht markiert, als bei mit dieser Antwort angefangen habe zu tippen :-) ) 

---

Hallo Wolfgang,bitte noch nicht löschen.

Ich vermute einmal es werden sich
nach der Einstellung des Fotos des Graphen
Abgründe auftun.

---

Hallo Georg,

ich bin für (Nicht-)Löschungen nicht zuständig :-)

---

Kann man auch Fragen beantworten, auch wenn sie gelöscht ist? Wäre toll wenn es ginge!! Und @Wolfgang , mache ich ;)

---

Keine Angst jetzt hast du hier sogar zwei Antworten ;) 

Nur die neue Frage wurde hierhin umgeleitet und Niki kann noch immer hier einen Stern vergeben. 

---

Oh sehr nett!! Vielen Dank ! :-)

---

(* Scherzmodus an *)
Ich bin für (Nicht-)Löschungen nicht zuständig :-)

also bist du für Löschungen zuständig ?
(* Scherzmodus aus *)

Answer 3

durch Raten findest Du 0 als Lösung.

Ansonsten mußt Du ein Näherungsverfahren z.B.Newton benutzen.

(Falls die Aufgabe wirklich so lautet?)

Comments

Dankeschön, und warum kann man es nicht von Hand lösen? Ist das unmöglich? Und für das Newtonverfahren muss man eine Wertetabelle anlegen oder?

---

und warum kann man es nicht von Hand lösen? Ist das unmöglich? 

Ja (mit Bordmitteln nicht möglich)

Und für das Newtonverfahren muss man eine Wertetabelle anlegen oder? 

Du mußt eine Skizze machen und einen sinnvollen Startwert ermitteln.

allgemeine Formel:

x _i+1= x_i - f(x_i)/f '(x_i)

das lernt man nicht in 5 Minuten

:-)

Answer 4

90=80e^{-0.05t}+10e^{0.038t}
9=8e^{-0.05t}+e^{0.038t}
t=0 kann man erraten, ist aber wahrscheinlich uninteressant ;)
Um eine Näherungslösung zu finden, kann man folgendes überlegen:
für größere t wird der Term 8*e^{-0.05t} recht klein, daher lassen wir den mal weg.
Dann hat man
9≈e^{0.038t} --> ln(9)/0.038 ≈ t ≈ 57.82

Nun ist

8e^{-0.05t}+e^{0.038t} für t = 57.82

≈9.44

also noch zu groß. Verändere daher den Wert t ein wenig um das Problem zu beheben!

Answer 5

x1=0 sieht man sofort.

Da die Faktoren mit nur 3 Nachkommastellen angegeben sind, soll vermutlich auch nur ein Näherungsverfahren angewendet werden.

Neben Bisektion (Iterationsrechner Beispiel 2)

funktioniert das Newton-Verfahren schneller:

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#10*exp(38*x/1000)+80*exp(-5*x/100)-90@Na=0;@B0]=56;//Startwert@Nb=@Bi];a=@Bi+1]=b-Fx(b)/@Lb);@N@Aa-b)%3C1e-13@N1@N0@N#

Nach 3 bis 4 Iterationsschritten hat man genügend Genauigkeit.

Interessante Zugabe:

Selbst beim Versuch, das exakt zu lösen, kommt man zu

x2 = 500*i*(2*Pi*n - i*log(a))
mit a=Polynom vom Grade 43 -> was auch nicht exakt explizit lösbar ist !!!

x2=56.388247159254087668529324724787188865...

und 56.38824715925408766868163... = (759 + 4929 e + 55740*Pi- 14392 * log(2))^{1/3}

stimmt zwar mit 18 Nachkommastellen überein, ist aber nicht Lösung dieser Gleichung