Extremwertaufgaben. Flächeninhalt

Question

Hallo. Ich brauche Hilfe Danke 

Answer 1

Hallo lindat! :-)

a)
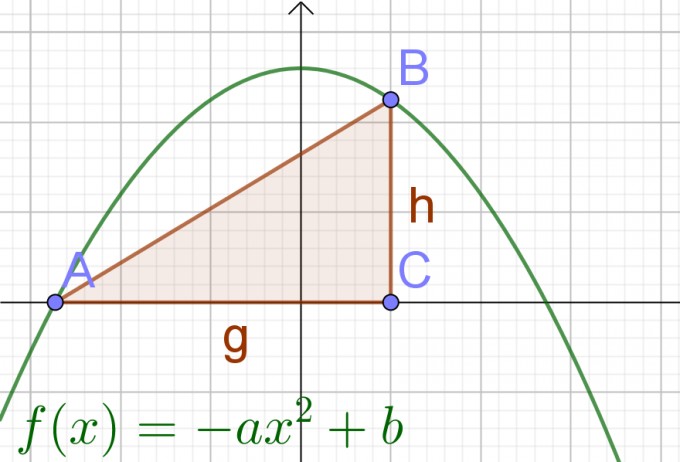
Die Grundseite g des Dreiecks verläuft vom Punkt A(x0|y0) bis zum Punkt C(x|y) und hat die Länge
g = x - x₀.
x₀ ist gleichzeitig eine Nullstelle:
-a(x₀)^2 + b = 0
-a(x₀)^2 = -b
x₀ = ±√(b/a)
Wir wählen x₀ = -√(b/a), weil die Nullstelle links von der y-Achse ist und können die Grundseite g so schreiben:
g = x - x₀
g = x - (-√(b/a)) 
g = x + √(b/a)
g ist damit von x abhängig, sodass wir  g(x) = x + √(b/a) schreiben können.

Die Höhe des Dreiecks ist h = -ax^2 + b und ebenfalls von x abhängig, wir
können h(x) = -ax^2 + b schreiben.

Den Flächeninhalt des Dreiecks berechnen wir mit der Formel A = g*h / 2.
Da unsere Grundseite sowie die Höhe von x abhängen, hängt auch der Flächeninhalt von x ab.
A(x) = g(x)*h(x) / 2
Wir setzen g(x) und h(x) in die Formel für den Flächeninhalt ein
A(x) = (x + √(b/a))*(-ax^2 + b) / 2
A(x) -1/2 ax^3 - 1/2 ax^2 √(b/a) + 1/2 bx + 1/2 b*√(b/a) und multiplizieren die Klammern aus

 
Der Flächeninhalt soll maximal sein, wir bilden die erste Ableitung
A'(x) = -3/2 ax^2 - ax*√(b/a) + b/2 und setzen sie Null.
A'(x) = 0
-3/2 ax^2 - ax*√(b/a) + b/2 = 0

Gesucht sind die Nullstellen von A'(x), wir bereiten die Gleichung für die Anwendung der PQ-Formel vor.
-3/2 ax^2 - ax*√(b/a) + b/2 = 0 | *(-2/(3a))
x^2 + 2/3*√(b/a)*x - b/(3a) = 0

Die Anwendung der PQ-Formel liefert uns zwei Ergebnisse
x₁ = 1/3*√(b/a)
x₂ = -√(b/a)
x₂ können wir nicht gebrauchen, denn das ist die Nullstelle x₀ der Funktion f(x) = -ax + b, die wir oben berechnet haben.
Darum setzen wir x₁ = 1/3*√(b/a) in die zweite Ableitung von A(x) ein.
A''(x) = -3*a(x) - √(ab)
A''(x₁) = -3*a(1/3*√(b/a)) - √(ab)
...
nach einigen Umformungen haben wir
A''(x₁) = -2√(ab)
A''(x₁) < 0
Die zweite Ableitung ist kleiner als Null, wir haben ein Maximum an der Stelle x1 = 1/3*√(b/a).
Damit ist der gesuchte Punkt B = (x₁ | f(x₁)) bzw. B = (1/3*√(b/a) | f(1/3*√(b/a))).

b)
Um die Formel für den maximalen Flächeninhalt zu bekommen, setzen wir x₁ = 1/3*√(b/a) in unsere Formel
A(x) = g(x)*h(x)/2 ein.
A(x₁) = -1/2 a(1/3*√(b/a))^3 - 1/2 a(1/3*√(b/a))^2 √(b/a) + 1/2 b*(1/3*√(b/a)) + 1/2 b*√(b/a)
...
nach einigen Umformungen haben wir
A(x₁) = (16/27)*b*√(b/a)

A''(x₁) = -3*a(1/3*√(b/a)) - √(ab)
A''(x₁) = -3*a(1/3*√(b/a)) - √(ab)
A''(x₁) = -a*√(b/a) - √(ab)
A''(x₁) = -√(ab) - √(ab)
A''(x₁) = -2√(ab)

A''(x₁) < 0 ==> Maximum an der Stelle x₁.
Damit ist B=(x₁|f(x₁)) bzw. B=(1/3*√(b/a)|f(1/3*√(b/a)))

Flächeninhalt
x₁ = 1/3*√(b/a) in A(x) einsetzen.
A(x₁) = -1/2 a(1/3*√(b/a))^3 - 1/2 a(1/3*√(b/a))^2 √(b/a) + 1/2 b*(1/3*√(b/a)) + 1/2 b*√(b/a)
A(x₁) = (16/27)*b*√(b/a)