Deckspiegelebenen, Drehachsen

Question

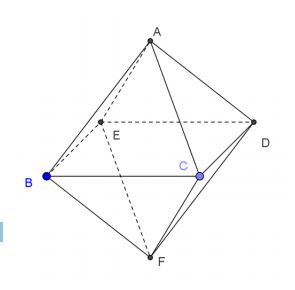
ABCDEF sei ein Oktaeder.

a) Wie viele Deckspiegelebenen besitzt
ABCDEF? Geben Sie alle diese Ebenen
durch ihre Fixecken, bzw. wenn diese
weniger als drei sind, durch zusätzliche
Fixpunkte an (z.b.,

ε₁ = ε(A,E,F,C) oder

ε₂ = ε(A,M_B,C,F), wobei M_B,C den Mittelpunkt von BC bezeichnet.)

b) Listen Sie alle zweizähligen Drehachsen
durch die Angabe von je zwei definierenden
Fixpunkten an (z.B.,

d₁ = g(M_B,C,M_E,D), wobei M_B,C und M_E,D die Mittelpunkte der Strecken BC und ED sind.)

c) Listen Sie alle dreizähligen Drehachsen durch die Angabe von je zwei
definierenden Fixpunkten auf (z.B.,

e₁ = g(M_B,C,A,M_E,F,D), wobei M_B,C,A und M_E,F,D die Mittelpunkte der Dreiecke BCA und EFD sind.)

Comments

Hallo Leonie,

kannst Du uns bitte sagen, wie bei Euch folgende Ausdrücke definiert sind:

- Deckspiegelebene

- Fixecke

- Fixpunkt einer Deckspiegelebene

- zwei- bzw. dreizählige Drehachse

Ist die Achse durch \(AF\) eine vierzählige Drehachse?

Gruß Werner