Hey Liebe Community,
Ich habe große Schwierigkeiten in Mathe, wie es sich aus dem Ergebnis meiner Prüfung deuten lässt (0 Punkte, gerdae ein mal 18% von 100% erreicht). D. h., anstatt das ich das Thema rasiert habe, hat mich das Thema rasiert. So nach unserer heutigen Jugendsprache.
Um es nun zu verstehen o. wenigstens nachvollziehen zu können, bitte ich euch/ jmd. mir das ein mal bitte bitte vorzurechnen/ erklären.
Die Aufg. schreibe ich hier gleich rein und alle zu benötigen Bilder füge ich gleich bei.
- - - - - - - - - - - - - - - - - - - - - - -
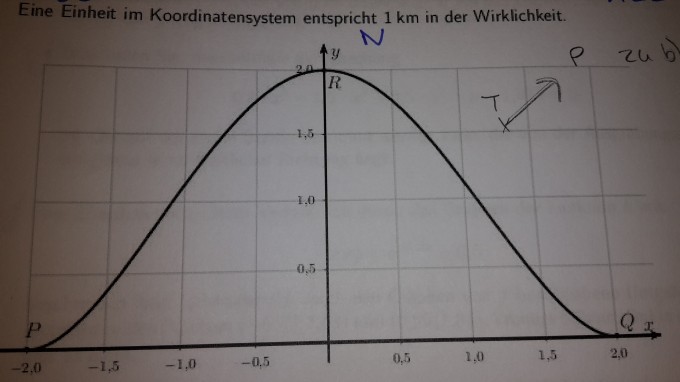
1) Das Städtchen Ickhausen soll eine nördliche Umgehungsstraße enthalten. Die Lage des Ortskerns sowie der Verlauf der alten und der neuen Straße können in einem Koordinatensystem veranschaulicht werden, wobei der Ortskern in dessen Ursprung liegt. Die alte Straße verläuft entlang der x-Achse in West-Ost-Richtung, genau durch die Ortsmitte. Die Umgehungsstraße soll die Punkte P(-2/1) und Q(2/0) über den Punkt R(0/2) verbinden und ohne Knick in den alten Straßenverlauf übergehen.
> 1 Längeneinheit, entspricht 1 Kilometer
1.1) Leiten Sie eine Gleichung einer ganzrationalen Funktion vierten Grades her, deren Graph symmetrisch zur y-Achse verläuft und den neuen Straßenverlauf beschreibt.
Verwenden Sie im Folgenden f(x) = 0,125 * x^4 - x^2 + 2
1.2) Weisen sie nach, dass R der nördlichste Punkt der Umgehungsstraße ist.
1.3) Zeigen sie rechnerisch, dass es genau einen Punkt S der Umgehungsstraße gibt, in dem die Linkskurve in eine Rechtskurve übergeht, wenn man den Ort von Westen kommend umfährt. Berechnen Sie die Koordination dieses Punktes.
2) Wegen archäologischer Funde auf der geplanten Umgehungsstraße im Punkt T(1/1,125) wird eine neue Streckenführung diskutiert. Diese lässt sich durch den Graphen der Funktion g mit g(x) = 0,5 * x^4 - 1,5 * x^3 + 0,5 * x^2 + 2
x E [0;2]
beschreiben.
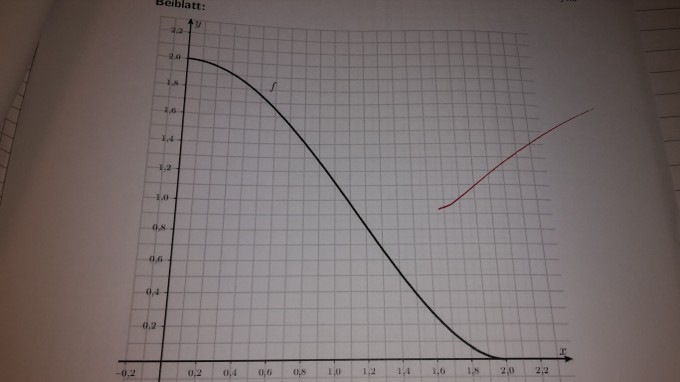
2.1) Zeichnen Sie den Graphen von g im Intervall [0;2] auf das Beiblatt, auf dem bereits der Graph von f eingezeichnet ist.
2.2) Begründen Sie, dass mithilfe der Gleichung 0,5 * x^4 - 1,5 * x^3 + 0,5 * x^2 - x + 1,875 = 0
der Ort auf der neuen Straße bestimmt werden kann, der von der Ausgrabungsstätte T aus genau in nordöstlicher Richtung liegt.
3) Eine Eisenbahnlinie, deren Verlauf sich durch den Graphen der Funktion h mit h(x) = e^-0,2x + 0,5 beschreiben lässt, schneidet die durch den Graphen von f beschriebene Umgehungsstraße ungefähr in den Punkten (-0,62/1,63) und (0,85/1,34). Weitere Schnittpunkte der Trassen gibt es nicht.
Das Gebiet das nördlich der Eisenbahnlienie von der ursprünglichen Umgehungsstraße und der Eisenbahnlinie eingeschlossen wird, wird für 7500000 Euro von der Stadt Ickhausen erworben. Bestimmen Sie den Quadratmeterpreis.
4)
4.1) Bestimmen Sie den durchschnittlichen Abstand der Punkte der durch den Graphen von f beschriebenen Umgehungsstraße in Nord-Süd-Richtung von der alten Ostdurchfahrt
4.2) Beschreiben Sie ein Verfahren, mit dem sich der kürzeste Abstand des Ursprunges zum Graphen von f im Intervall [0;2] ermitteln lässt.
Vielen Dnk für die Hilfe!