Beweisen mit Hilfe des Grenzwerts

Question

Beweisen Sie mit Hilfe des Grenzwerts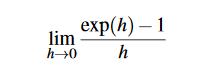

aus der vorigen Aufgabe und der Funktionalgleichung, dass die Exponentialfunktion uberall differenzierbar ist und

∀x∈R: exp′(x) =exp(x)

Hinweis:
Sie dürfen die allgemeine Ableitungsregel für Potenzreihen nicht benutzen

Answer 1

L'Hospital wenn ihr hattet.

lim (h --> 0) (e^{h} - 1) / h

= lim (h --> 0) e^{h} / 1 = e^{0} / 1 = 1/1 = 1

Comments

Wenn man gerade zeigen soll, dass e^{x} ' = e^x ist, so kann man nicht einfach mal die Ableitung der Exponentilafunktion als vorausgesetzt annehmen und l'hospital anwenden. Das ist dann irgendwie sinnlos ;). Zumal der Grenzwert aus der vorherigen Aufgabe auch schon vorgegeben ist.

Answer 2

Tipp: \(\dfrac{\exp(x_0+h)-\exp(x_0)}h=\dfrac{\exp(x_0)\cdot\exp(h)-\exp(x_0)}h=\exp(x_0)\cdot\dfrac{\exp(h)-1}h\).