Aufgabe:
Ein rechteckiges Fenster eines Hauses sei \( 2 \mathrm{~m} \) breit und \( 1,50 \mathrm{~m} \) hoch. Direkt an seiner Oberkante schliebe sich innen die Zimmerdecke an. Zur Schattenspende bei hochstehender Sonne im Sommer einerseits sowie zur Ausnutzung des Sonnenlichtes als indirekter Zimmerbeleuchtung in der lichtarmen Jahreszeit andererseits sei an der Ober- bzw. Unterkante des Fensters jeweils ein rechteckiger sog. Solarfaltladen aus einem reflektierenden Material von der Breite des Fensters und einer Tiefe von \( 1 \mathrm{~m} \) angebracht, der in einem Winkel von \( 30^{\circ} \) nach oben bzw. unten gekippt sei. Die Verbindungslinie von der (punktformigen) Sonne zum Haus liege in einer Ebene senkrecht zu unserem Fenster. In welcher Richtung muB die Sonne stehen, damit mit Hilfe des unteren Solarfaltladens an der Zimmerdecke ein Bereich indirekt bestrahlt wird, der genau an der Außenkante der Zimmerdecke beginnt?
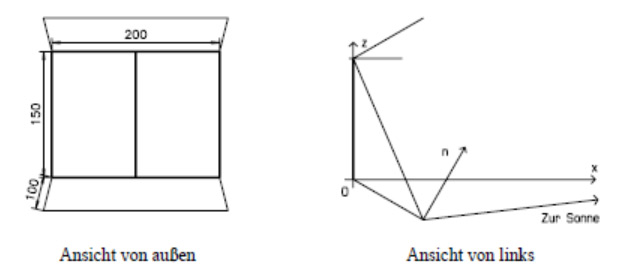
Hinweis: Man definiere ein geeignetes kartesisches Koordinatensystem, etwa mit dem Nullpunkt in der linken unteren Fensterecke, und lege die Achsen so, dass sich das Fenster in einer der Koordinatenebenen befindet. Dann berechne man den Vektor sin Richtung Sonne bzgl. dieses Koordinatensystems.