Berechne die Steigungen in den Schnittpunkten mit der x-Achse (mit der y-Achse)?!

Question

a) f(x)=4x-x³

b) f(x)=3x²-(x hoch4; Geht bei meiner Tastatur nicht.=

Comments

BITTE brauch' Hilfe dabei :(

---

Hi

Die Hochzahlen kannst Du mit dem " ^ " Zeichen machen (s. Bild). Wenn Du die Taste drückst erscheint das Zeichen aber erst, wenn Du den nächsten Buchstaben schreibst. Wenn Du eine Klammer um den Exponenten machst, dann kannst Du auch kompliziertere Ausdrücke als Exponent schreiben. Du schreibst dann erstmal die Basis hin, dann drückst Du " ^ ", dann kommt die Klammer auf, dann der Exponent und dann Klammer zu. Der Texteditor hier erkennt das dann und wandelt das um.

lg JR

---

Danke erstmal dafür :)

Nur war die eigentliche Aufgabe dabei:

Berechne die Steigungen in den Schnittpunkten mit der x-Achse (mit der y-Achse):

a) f(x)=4x-x³

b) f(x)=3x²-x^4

---

Tut mir leid. Bin an der Stelle nicht mehr ganz fertig geworden weil ich unterbrochen wurde. Ich habe die Aufgaben noch ergänzt.

Answer 1

a) f(x) = 4x-x^3

Schnitt mit x-Achse -> y = 0:
0 = 4*x-x^3; //x ausklammern
0 = x*(4 -x^2); -> x1 = 0;
für x =/=0;
0 = (2-x)*(2+x); //3. binomische Formel
-> x2 = 2; x3 = -2);

SP1(0|0);  SP2(2|0);  SP3(-2|0);

Schnitt mit der y-Achse -> x = 0:
f(x=0) = 0;

SP4(0|0)

Steigung:
f'(x) = 4-3*x^2;
f'(x=0) = 4;
f'(x=2) = -8;
f'(x=-2) = -8

 

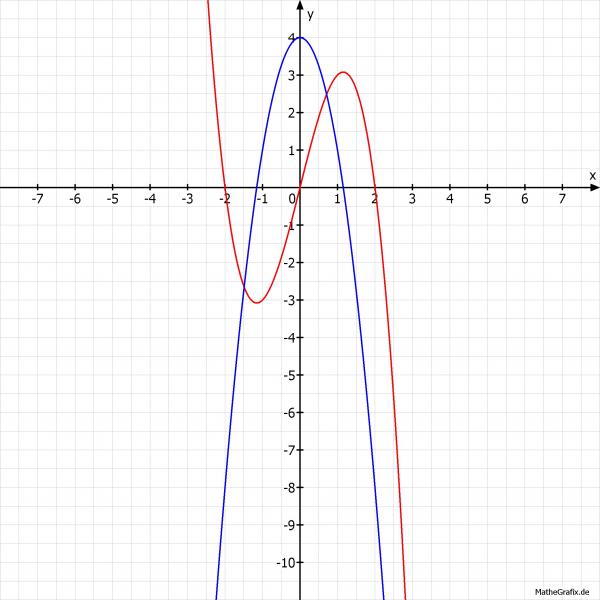
b) f(x) = 3*x^2-x^4;

Schnitt mit der x-Achse -> y = 0:
3*x^2-x^4 = 0; //x^2 ausklammern
x^2*(3*-x^2) = 0; // -> x1 = x2 =0; //Doppelte Nullstelle
für x=/=0:
x^2 = 3; // -> x3 = -sqrt(3); x4 = sqrt(3);

SP1(0|0);  SP2(-sqrt(3)|0);  SP3(sqrt(3)|0);

Schnittpunkt mit y-Achse -> x = 0:
f(x=0) = 0;

SP4(0|0); //also identisch mit Schnitppunkt SP1(0|0);

Steigung:
f'(x) = 6*x-4x^3;
f'(x=0) = 0;
f'(x=sqrt(3)) = -6*sqrt(3) ≈ -10,4;
f'(x=-sqrt(3)) = 6*sqrt(3) ≈ 10,4;

 

lg JR

Answer 2

a)

f(x) = 4·x - x^3 = x·(4 - x^2)

f'(x) = 4 - 3·x^2

Nullstellen f(x) = 0
x·(4 - x^2) = 0
x1 = 0, x2 = -2, x3 = 2

f'(0) = 4
Steigung im Schnittpunkt mit x und y-Achse ist 4

f'(-2) -8
f'(2) = -8
An den anderen beiden Schnittpunkten mit der x-Achse ist die Steigung -8.

Comments

b)

f(x) = 3·x^2 - x^4 = x^2·(3 - x^2)

f'(x) = 6·x - 4·x^3

Nullstellen f(x) = 0
x^2·(3 - x^2) = 0
x1 = 0, x2 = -√3, x3 = √3

f'(0) = 0
f'(-√3) = 6·√3
f'(√3) = -6·√3

---

SUPER, alles SUPER!!!