Hi
Ich geh mal davon aus, dass die Dreiecke ähnlich und gleichseitig sind:
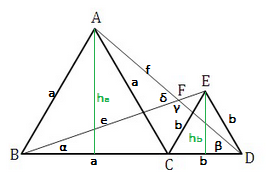
a) Bestimme das Verhältnis AD : BE.
ha= a/2*sqrt(3); //Pythagoras
hb= b/2*sqrt(3);
e2 = (a+b/2) +hb; //Pythagoras, \(e = \overline{BE} \)
e = sqrt(a2 +ab +b2);
f2 = (b+a/2) +ha; //Pythagoras, \(f = \overline{AD} \)
f = sqrt(a2 +ab +b2);
f/e = 1;
b) Bestimme den Winkel ∠AFB.
tan(α) = hb / (a+b/2);
α = arctan{ b*sqrt(3) / (2a +b) };
tan(β) = ha / (b+a/2);
β = arctan{ a*sqrt(3) / (2b +a) };
γ = 180° -α -β;
δ = α +β = arctan{ b*sqrt(3) / (2a +b) } + arctan{ a*sqrt(3) / (2b +a) };
Vielleicht gibt es für die b) noch eine elegantere Lösung. Die hab ich aber bisher nicht entdeckt. Jedenfalls kannst Du mit der Formel für δ (fett geschrieben) den Winkel in Abhängigkeit der Seitenlängen der beiden ähnlichen, gleichseitigen Dreiecke bestimmen.
lg JR