Funktionsschar - Beurteilung von Aussagen

Question

gilt immer - gilt nie - es kommt drauf an 

Gegeben ist die Funktionenschar fa mit fa(x) = ax^2 + ax - 6 (a ungleich 0).

Beurteile ob folgende Aussagen immer gelten, nie gelten oder von dem Wert des Parameters a abhängen. Begründe.

a) Der Graph von fa hat eine Wendestelle.

b) Der Graph von fa hat einen Hochpunkt 

c) Der Graph von fa schneidet die y-Achse bei (0/0)

d) Der Graph von fa schneidet die x-Achse zweimal

Answer 1

a) ich würde sagen stimmt nicht, da es eine Parabel ist und die f´´(x)=0 nie existiert, oder doch?

b) kommt drauf an, wenn a negativ ist, dann ja, wenn positiv ist, dann nicht

c) das weiss ich nicht genau.

d) a muss positiv sein.

Ich hoffe, ich konnte dir weiter helfen.

Smitty

Comments

EDIT zu c): Mein Ansatz wäre: Punkt P(0|0) einsetzen.

$$0=a\cdot 0^2+0a-6\\o\neq 6$$

Ob man das so machen darf, weiß ich nicht genau.

---

An smitty,
a) ich würde sagen stimmt nicht, da es eine Parabel ist und die f´´(x)=0 nie existiert, oder doch?

Die Funktion ist eine Parabel.
Parabeln haben keinen Wendepunkt.
Erst Funktionen 3.Grades.

b) kommt drauf an, wenn a negativ ist, dann ja, wenn positiv ist, dann nicht
Stimmt. Mathematisch.
f = ax^2
f ´ = 2ax ( Extrempunkt )
f ´´ = 2a ( Krümmung )

Ist a positiv dann ist der Extrempunkt ein
f ´´ = positiv. Krümmung konvex. Tiefpunkt.
Eine nach oben geöffnete Parabel
Beispiel : f ( x ) = 2 * x^2

Ist a negativ dann ist der Extrempunkt ein
f ´´ = negativ. Krümmung konkav. Hochpunkt.
Eine nach unten geöffnete Parabel.
Beispiel : f ( x ) = -2 * x^2

c)  Der Graph von fa schneidet die y-Achse
bei (0/0) . Das weiss ich nicht genau.

fa(x) = ax^2 + a*x - 6
fa(0) = a*0^2 + a*0x - 6  = -6
Schnittpunkt y-Achse ( 0 | -6 )

d) a muss positiv sein.
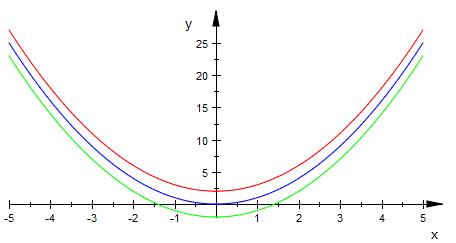
Allgemein : Parabeln können
- 1 Schnittpunkt haben ( blau )
- 2 Schittpunkte haben (  grün )
- keinen Schnittpunkt haben ( rot )

fa(x) = ax^2 + a*x - 6
Nullstellen
ax^2 + a^x - 6 = 0
mit Mitternachts, pq-Formel, quadr.Ergänzung
lösen.
x = ± √ [ ( a^2 + 24a ) / ( 4a ) ] -1/2

Fallunterscheidung allgemein für
x = ± √ term
Ist term
positiv : gibt es zwei Lösungen ( grün )
null : gib es eine Lösung ( blau )
negativ : keine Lösung ( rot )

Jetzt die Fallunterscheidung für obige Formel
durchführen
z.B. positiv : a = .. oder a > ...

---

a) stimmt wenn a=x ist

Dann : fx(x) = x^3+x^2-6

---

Es hat schon Charme, wenn Meinungsäußerungen von keinerlei Sachverstand getrübt werden.

---

Könnte aber vielleicht auch Anlass sein, über die Symmetrie der Gleichheitsrelation nachzudenken.

---

Warum ist es denn nicht möglich dass a = x ist

---

x ist eine Variable. D.h. nimmt unendlich viele verschiedene Werte an. Und für jeden Wert von x gibt es einen Funktionswert y.

a ist ein Parameter. Parameter stehen für eine feste Zahl. Für jeden Wert von a erhältst du also eine andere Funktion.

---

Hallo ohig,

f _a (x) = a*x^2 + a*x - 6
ist eine Funktionsschar. Die Funktionen unterscheiden
sich im Wert von a.
Beispiel
a = 2
f ₂ (x) = 2*x^2 + 2*x - 6
oder
a = 3
f ₃ (x) = 3*x^2 + 3*x - 6

Der Wert  von a darf darf innerhalb von Berechnungen
mit der Funktion nicht mehr geändert werden.

Answer 2

a) Der Graph von fa hat eine Wendestelle.

Eine Funktion 2. Grades ist eine Parabel und hat keine Wendestelle.

b) Der Graph von fa hat einen Hochpunkt

Wenn a < 0 ist, ist der Graph eine nach unten geöffnete Parabel mit einem Hochpunkt.

c) Der Graph von fa schneidet die y-Achse bei (0 | 0)

fa(0) = a·0^2 + a·0 - 6 = -6
Der Graph geht nie durch den Ursprung.

d) Der Graph von fa schneidet die x-Achse zweimal

fa(x) = a·x^2 + a·x - 6 = 0
x^2 + x - 6/a = 0
x = - 1/2 ± √(1/4 + 6/a)

Hat zwei Lösungen für
1/4 + 6/a > 0
6/a > - 1/4

Fall 1: a > 0
6/a > - 1/4 → a > -24 → a > 0

Fall 2: a < 0
6/a > - 1/4 → a < -24