Wie linearisiere ich? Verständnisproblem, wann Ableitungen wegfallen. 1) y'' + y = 4u^2

Question

Nachtrag: " Ja, u soll u(t) und eine lineare Funktion von t sein."

Folgende Funktionen möchte ich linearisieren um y = 2 und u = 0,5 

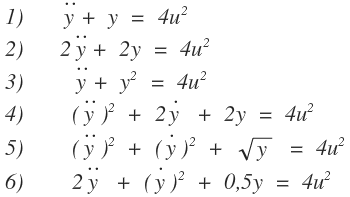
Ich bin total durcheinander. Der Professor hat etwas erklärt. Z.Bsp. wenn es geklammert ist wie bei (y'')^2 und potenziert, dass die Ableitung wegfällt. Ich kriege die Erklärung gedanklich auch nicht mehr zusammen.

Ich habe Folgendes versucht:

Und die 6) ganz unten

Ich bin über jeden Hinweis dankbar!

Grüße, Michael

Comments

Hat sich das hier https://www.mathelounge.de/518164/linearisierung-einer-funktion-2x-5x-4y-betriebspunkt-hat-y0 inzwischen geklärt? Erscheint immer noch hier https://www.mathelounge.de/unanswered

---

Hallo Michael,

kann man davon ausgehen, dass \(u=u(t)\) eine lineare Funktion von \(t\) ist?

---

Hallo Werner,

vielen Dank für die Nachricht. Ja, u soll u(t) und eine lineare Funktion von t sein.

---

Hallo Lu,

vielen Dank für die Nachricht. Nein, das hat sich leider auch noch nicht geklärt.

---

Ich weiß, dass ich die Taylor - Näherung anwenden muss. Muss ich demnach noch 4u^2 auf die linke Seite bringen? 

Also das ist die Formel, mit der es funktionieren soll:

Also bei mir müsste dann immer (y,u) stehen

Könnt ihr mir damit und mit den Bildern von oben erklären, wie ich die Funktionen richtig linearisiere?

---

Deine Rechnungen sind mir (immer noch) zu hoch. Wenn y als Funktion von t linear wäre, dann wäre bereits d^2/dt^2 y = 0 . Aber davon steht nichts. 

Vielleicht hat jemand anders bald eine Idee. 

---

Die DGL an sich ist nicht linear. Also alle y Terme sind als nichtlinear zu behandeln. Und bei 4u² bin ich mir nicht sicher.

Ich dachte, u(t) alleinstehend muss eine lineare Funktion sein. Dann kommt aber das Quadrat hinzu..