Hallo davinci,
Gehe einfach konsequent vor und setze jede Information in eine geometrische Bedeutung um. Eine bildliche Vorstellung hilft ungemein. Da der Punkt \(A\) jedes mal vorkommt, beginne mit \(A\). Nehme ein Stück Papier (mit Kästchen) mache einen Punkt in der Mitte und nenne ihn \(A\). $$|\vec{OA}| = 2$$ Der Punkt \(O\) liegt auf einem Kreis mit Radius 2 um \(A\). Zeichne einen Kreis um \(A\).
$$\vec{AB} = \begin{pmatrix} -3\\ 4\end{pmatrix}$$ das ist eindeutig. \(B\) kann man direkt einzeichnen, wenn \(A\) gegeben ist.
$$ |\vec{AC}|= \frac12|\vec{AB}|$$ \(C\) liegt auf einem Kreis um \(A\), der durch den Mittelpunkt der Strecke \(AB\) geht. Zeichne den Kreis.
$$\vec{OC} - \vec{OA} = \begin{pmatrix} 0\\ y\end{pmatrix} \quad y \in \mathbb{R}$$ das kann man noch etwas umformen, da \(\vec{OC}=-\vec{CO}\)
$$\vec{OC} - \vec{OA} = -\vec{CO} - \vec{OA} = -(\vec{CO} + \vec{OA}) = -\vec{CA}$$ D.h. der Punkt \(C\) hat die gleiche X-Position wie \(A\) - liegt also auf einer vertikalen Geraden durch \(A\). Zeichne die Gerade ein, ihre Schnittpunkte mit dem zweiten Kreis um \(A\) sind die beiden gesuchten Möglichkeiten für den Punkt \(C\). Dein Papier sollte nun ungefähr so aussehen (ohne die blauen Pfeile):
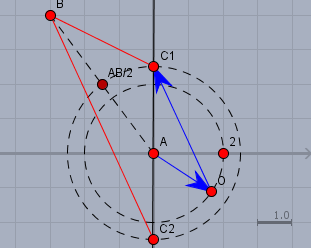
Die roten Strecken sind die gesuchten Längen
$$|\vec{BC_1}| =\frac32 \sqrt{5} \approx3,35 \quad |\vec{BC_2}| = \frac12\sqrt{205} \approx 7,15$$ falls Du Fragen hast, wie ich das berechne habe, so melde Dich bitte.
Gruß Werner