Hallo Judith,
setze für \(z\) zunächst \(z=a+bi\). Und forme die Brüche so um, dass im Nenner keine Imaginäranteile mehr stehen. Es ist
$$\frac{2z - 2i}{z+1} = \frac{2a + 2bi - 2i}{a+bi +1 } = \frac{(2a + (2b - 2)i)((a+1)-bi)}{((a+1)+bi)((a+1)-bi) } = \frac{2a(a+1)+b(2b-2) + i((2b-2)(a+1) - 2ab) }{(a+1)^2 + b^2}$$ mit \( \text{Im}\left( \frac{2z-2i}{z+1}\right)\ge 1\) ist dann
$$\text{Im}\left( \frac{2z-2i}{z+1}\right) = \frac{(2b-2)(a+1) - 2ab }{(a+1)^2 + b^2} \ge 1$$ da der Nenner immer >0 ist, kann ich ohne Fallunterscheidung mit dem Nenner multiplizieren
$$(2b-2)(a+1) - 2ab \ge (a+1)^2 + b^2$$ $$ 2ab + 2b - 2a - 2- 2ab \ge a^2 + 2a + 1 + b^2$$ $$ 0 \ge (a^2 + 4a + 4) -2 + (b^2 - 2b + 1)$$ $$ 0 \ge (a+2)^2 -2 + (b - 1)^2$$ $$ (b - 1)^2 + (a+2)^2 \le 2 $$ das ist eine Kreisfläche mit dem Mittelpunkt bei \((-2|1)\) mit dem Radius \(\sqrt{2}\).
Gehe entsprechend mit der zweiten Ungleichung vor. Hier ist die Lösung eine Fläche die sich zwischen vier Hyperbelästen befindet. ich habe Dir das noch mal aufgezeichnet.
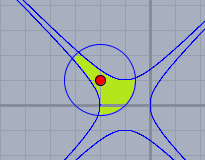
die grün markierte Fläche inklusive des Rands ist die graphische Darstellung der Lösung in der Gauß'schen Zahlenebene. Falls Du dazu noch Fragen hast, so melde Dich bitte.
Gruß Werner