Berechnung von Körpern: 3 Kugeln

Question

In einer Kiste liegen drei gleich große Kugeln mit einem Radius von 5 cm so, dass sie sich berühren und ihre Mittelpunkte ein gleichseitiges Dreieck bilden. Steffi packt in die Mitte eine vierte Kugel, die gerade zwischen den drei Kugeln durchrutscht. Wie groß war der Radius dieser Kugel höchstens?

Comments

Die Aufgabe ist so gut fotografiert worden, dass es völlig egal ist, dass sie falsch fotografiert worden ist... :-)

Answer 1

Hallo Emre,

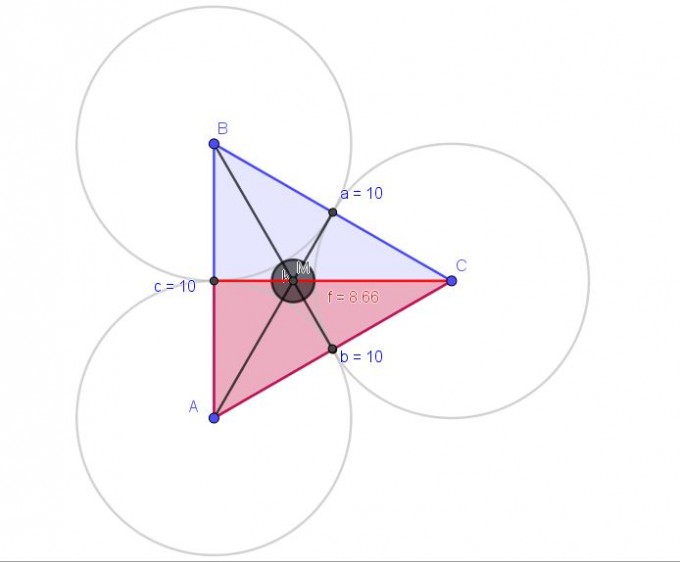
der Schwerpunkt eines gleichseitigen Dreiecks ergibt sich aus den Schnittpunkt der Seitenhalbierenden, die in diesem Fall auch die Höhen des Dreiecks bilden.

Dieser Schwerpunkt ist der Mittelpunkt der gesuchten 4. Kugel.

Wie Oswald schon sagte, berechnest du die Längen der Höhen mit dem Satz des Pythagoras (hier f = 8,66). Der Schnitt-/Mittelpunkt teilt die Seitenhalbierenden/Höhen im Verhältnis zwei zu eins, also zwei Teilstrecken mit den Längen 2,887 und 5,774.

Wenn du von 5,774 den Radius der Kugeln = 5 abziehst, hast du den Radius der gesuchten Kugel = 0,774.

Gruß, Silvia

Comments

Hier eine Formel zum angegebenen Lösungsweg:

$$ r = \dfrac 23 \cdot \sqrt{\left(2R\right)^2-R^2}-R $$Vereinfachen ergibt dann

$$ r = \left(\dfrac 23 \cdot \sqrt{3}-1\right)\cdot R $$wobei jeweils \(r\) der hier gesuchte maximale Radius der kleinen Kugel und \(R\) der hier mit 5 angegebene Radius der großen Kugeln ist.

Answer 2

10 ^2 = 5^2 + h(c)  ^2
h(c) = 8.660 cm

Alle Winkel im Dreieck sind 60 °
Der Winkel von Punkt A bis zur Mitte der
kleinen Kugel ist 30 °
tan ( 30 ) = ( Mitte Kugel bis Strecke c ) / 5
Mitte Kugel bis Strecke c = 2.887 cm
oberer Teil von h(c) = 8.660 - 2.887 = 5.773
Radius der kleinen Kugel = 5.773 - 5 = 0.773

Answer 3

> Steffi packt in die Mitte eine vierte Kugel, die gerade zwischen den drei Kugeln durchrutscht.

Der Mittelpunkt von Steffies Kugel bildet zusammen mit den Mittelpunkten von zwei Kugeln ein gleichschenkliges Dreieck. Gleichschenklige Dreiecke lassen sich in zwei kongruente rechtwinklige Dreiecke unterteilen. Stelle den Satz des Pythagoras für eines dieser Dreiecke auf.

> und ihre Mittelpunkte ein gleichseitiges Dreieck bilden.

Jedes gleichseitige Dreieck ist auch gleichschenklig. Also ist ebenfalls obige Unterteilung möglich. Stelle den Satz des Pythagoras für eines dieser Dreiecke auf.

Comments

@oswald: liege ich dann mit meiner Rechnung (mit Deinem pythagoreischen Vorschlag) bei einem max. Radius von 0,625 cm richtig?

---

Ich habe 10/√3 - 5 raus.