Aufgabe:
Aus drei Blechplatten soll eine 2 m lange Regenrinne geformt werden (siehe Abbildung). Die Rinne soll eine Querschnittsfläche von \( 250 \mathrm{cm}^{2} \) besitzen.
Wie müssen Höhe h und Breite b gewählt werden, wenn der Materialverbrauch möglichst niedrig sein soll?
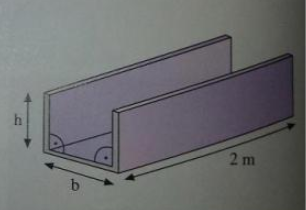
Ich verstehe das so, dass b * 2 m = 250 cm2 sein sollen, woraus folgt: b = 250 cm2 / 200 cm = 1,25 cm.
Wenn ich jetzt minimalen Materialverbrauch anstrebe, nehme ich einfach einen Nanometer oder so als h.
Das scheint aber unsinnig.
Durchgerechnet:
Material = 1,25 cm * 200 cm ("Bodenplatte) + 2 * 200 cm * h (die beiden "Seitenplatten").
Also
f(h) = 1,25 cm * 200 cm + 2 * 200 cm * h
f'(h) = 2 * 200 cm | dies wird natürlich niemals = 0
Ist folgende Überlegung korrekt?
Die Regenrinne soll ein Volumen von 250 cm3 haben.
Dann hätte man
V = 250 = b * h * 200
Aufgelöst nach b:
b = 250/(200 * h)
A = b * 200 ("Bodenplatte") + 2 * h * 200 ("Seitenplatten")
b eingesetzt:
A = f(h) = 250/(200 * h) * 200 + 2 * h * 200 = 250 * h-1 + 400h
f'(h) = 400 - 250 * h-2
Notwendige Bedingung für Minimum f'(h) = 0
400 - 250 * h-2 = 0
400 = 250 * h-2 | : 250
1,6 = 1/h2 | * h2
1,6 * h2 = 1
h2 = 1/1,6
h ≈ 0,79
Dann hätten wir als Materialverbrauch ca.
A = b * 200 + 2 * h * 200 =
b * 200 + 2 * 0,79 * 200 =
250 / (200 * 0,79) * 200 + 2 * 0,79 * 200 ≈
632,46
Nehme ich zum Vergleich h = 0,6, so komme ich auf:
250 / (200 * 0,6) * 200 + 2 * 0,6 * 200 ≈
656,67
und h = 0,9:
250 / (200 * 0,9) * 200 + 2 * 09 * 200 ≈
637,78
Ich bitte um Eure Meinungen.