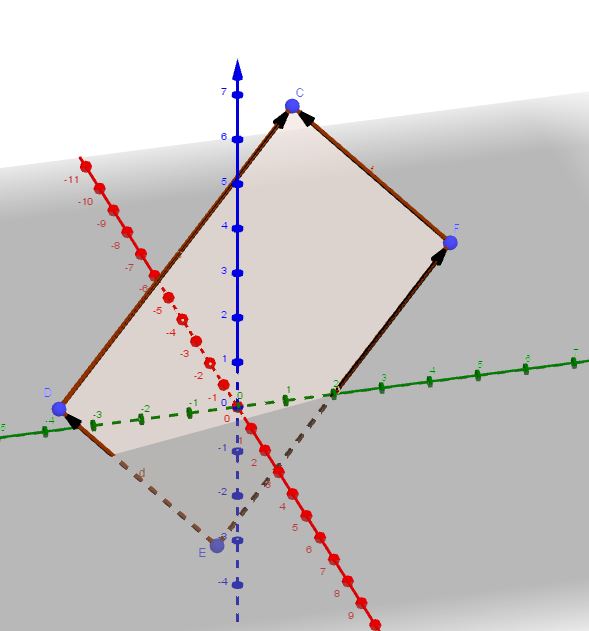
Kennzeichnend für ein Parallelogramm ist, dass die jeweils gegenüberliegenden Seiten parallel zueinander liegen und gleich lang sind.
du berechnest also die Richtungsvektoren ED und FC und vergleichst sie miteinander (du könntest auch DE und CF nehmen), das Gleiche machst du mit den anderen beiden Vektoren DC und EF. Um den RV ED zu bilden, subtrahierst du die Koordinaten des Punktes E von denen des Punktes D. So gehst du auch bei der Bestimmung der anderen drei Vektoren vor. Hier die Rechnung zu den ersten beiden Vektoren. Solltest du Probleme bei den anderen beiden haben, bitte melden. (Zur Kontrolle: RV =(-4|6|4))
$$ \vec{ED}\begin{pmatrix} 1 - 2\\-4 - (-1)\\1 - (-2) \end{pmatrix}=\begin{pmatrix} -1\\-3\\3 \end{pmatrix} $$
$$ \vec{FC}\begin{pmatrix} -3 - (-2)\\2 - 5\\5 - 2 \end{pmatrix}=\begin{pmatrix} -1\\-3\\3 \end{pmatrix} $$
Gruß, Silvia