Aufgabe 2 :
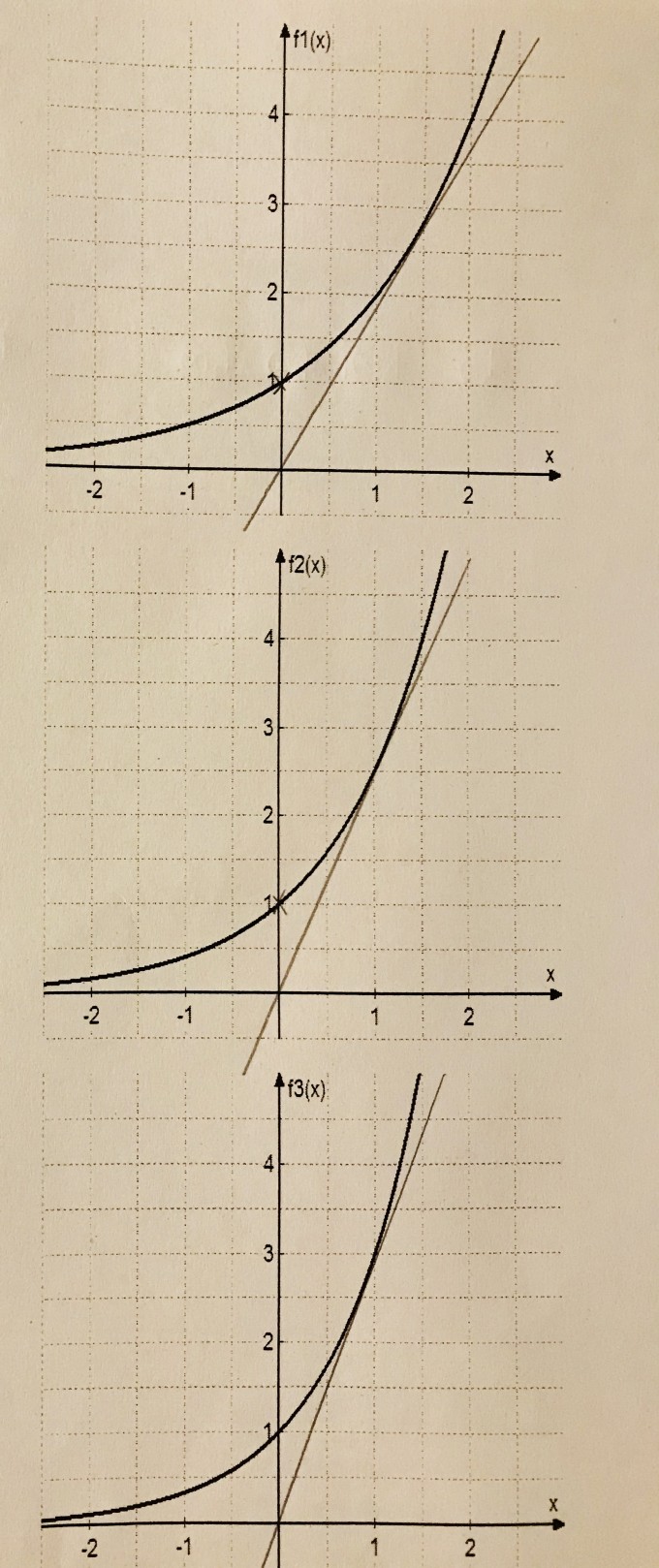
Links sind drei Graphen von Exponentialfunktionen f1,f2 und f3 dargestellt. Es gilt
f1(x)=a1^x
f2(x)=a2^x
f3(x)=a3^x
a) Ermitteln Sie a1,a2 und a3 und somit die Funktionsterme
b) Zeichnen Sie in allen drei Fällen die Tangente an der Stelle x=0 ein und ermitteln Sie die jeweilige Steigung!
c) Berechnen Sie die drei Steigungen aus Teil b) unter Benutzung der jeweiligen Basis aus Teil a) mit dem Taschenrechner!
TR: Graph eingeben
-Graph analysieren
-dy/dx
Hinweis: dy/dx=d/dx f(x) (gesprochen: d nach dx) ist die Ableitung von y bzw. f(x) nach x )
Zusammenstellung der Ergebnisse:
f1(x)=
f‘1(0)=
f2(x)=
f‘2(0)=
f3(x)=
f‘3(0)=
Aufgabe 3:
Ermitteln Sie mithilfe des Taschenrechners durch Ausprobieren eine Basis a für eine Exponentialfunktion mit f(x)=a^x, sodass f‘(0)=1 ist!
Hier noch die Graphen zu der Frage. Kann mir jmd. helfen?