neutrales und inverses Element in ℚ[√a]*

Question

ich brauche bei einer Aufgabe Hilfe.

 

Für a∈ℕ Quadrat-frei betrachtet man die Menge

ℚ[√a]* := {x+y√a: x,y∈ℚ} - {0}.

Zeigen Sie, dass ℚ[√a]* mit der Verknüpfung

(x₁+y₁√a)*(x₂+y₂√a) = x₁x₂+y₁y₂a+ (x₁y₂+x₂y₁)√a

eine Gruppe bildet.

 

Die Assoziativität habe ich schon gezeigt, aber bei dem neutralen und inversen Element habe ich Probleme. Wie zeigt man die?

Danke

Answer 1

Wenn du etwas hast, das stimmt, ist die Existenz bewiesen.

Ich nehme mal das Resultat von deinem Kommilitonen und schreibe Wa für Wurzel aus a.

Und nehme an, dass für ein beliebiges Element dieser Menge z= s+tWa ein Inverses z^-1 = u+vWa existiert.

So gilt

(s+tWa)(u+vWa) = 1 + 0Wa                  |Nun rechne ich u+vWa aus.

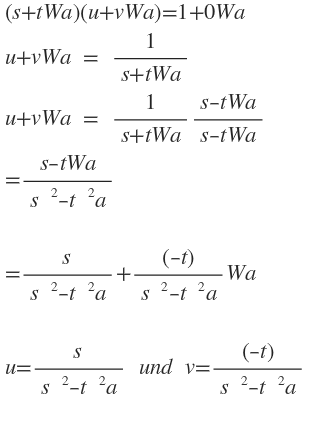
u und v sind rationale Zahlen, da sie aus solchen aufgebaut sind.

Nun kannst du, das Inverse einsetzen und hoffen dass sowohl z*z^-1 als auch z^-1*z das neutrale Element ergeben.

Anhang: Latex-Text der Formeleingabe:

(s+tWa)(u+vWa)=1+0Wa\\ u+vWa\quad =\quad \frac { 1 }{ s+tWa } \\ u+vWa\quad =\quad \frac { 1 }{ s+tWa } \frac { s-tWa }{ s-tWa } \\ =\frac { s-tWa }{ s{ \quad  }^{ 2 }-t{ \quad  }^{ 2 }a } \\ \\ =\frac { s }{ s{ \quad  }^{ 2 }-t{ \quad  }^{ 2 }a } +\frac { (-t) }{ s{ \quad  }^{ 2 }-t{ \quad  }^{ 2 }a } Wa\\ \\ u=\frac { s }{ s{ \quad  }^{ 2 }-t{ \quad  }^{ 2 }a } \quad und\quad v=\frac { (-t) }{ s{ \quad  }^{ 2 }-t{ \quad  }^{ 2 }a } \\ 

Comments

Du musst hier sicher noch ergänzen, weshalb im Nenner nicht 0 stehen kann.

Dazu Folgendes:

Nach Voraussetzung ist s oder t  ungleich 0. Wenn nur s oder nur t nicht 0 sind, ist der Nenner nicht Null.

Bleibt s≠0 und t≠0:

Beweis durch Widerspruch:

Annahme s^2 = t^2 a.

Da a quadratfrei ist, führt jede Primfaktorzerlegung (selbst als Bruch) von s^2 und t^2 a bei t^2 a zu mindestens einer ungeraden Potenz einer Primzahl, was bei s^2 nicht möglich ist.

Somit ist die Annahme s^2 = t^2 a falsch und der nenner tatsächlich nie 0.

Jetzt fehlt tatsächlich nur noch die Ausmultiplikation der Terme. vgl. oben.

Answer 2

Grüße vom Kommilitonen:

Du verknüpfst halt stur mit (x₁+y₁*Wurzel(a))x(x₂+y₂Wurzel(a))=(x₁+y₁*Wurzel(a)), wenn (x₂+y₂Wurzel(a)) kriegst dann eine Gleichung die du in 2 aufteilen kannst(einmal für den x-Wert und für den y-Wert).
Wenn du e dadurch hast kannste das nochmal probieren, aber ich schätze, dass es kein inverses Element gibt.