Hallo Sliverdart,
Thomas Simpson hatte wohl heraus gefunden, wie man das Volumen eines beliebigen Prismatoiden berechnet. So ein Prismatoiden kann ganz schön kompliziert aussehen - z.B. so (klick auf das Bild):
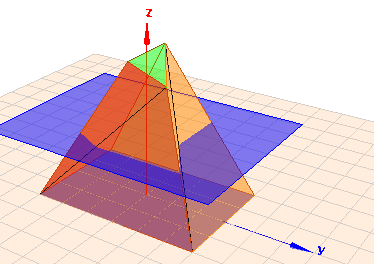
Denke Dir die blaue Fläche zunächst mal weg. Die kommt später. Oben siehst Du einen Prismatoiden, dessen Grundfläche ein Rechteck und dessen Deckfläche ein Dreieck ist. Beide Flächen liegen parallel und die Seitenflächen bestehen nur aus Dreiecken und Trapezen.
Wenn man nun das Volumen so eines Körpers berechnen will, so kann man sich ihn in ganz viele beliebig dünne waagerechte Scheiben zerschnitten denken, die alle die Höhe \(\Delta h\) haben. Jede dieser Scheiben habe die Fläche \(A\) und da diese Fläche von der Position im Prismatoiden abhängt, ist diese eine Funktion der Höhe - also \(A(h)\). Eine Scheibe in der Höhe \(h\) hat demnach ein Volumen \(\Delta V=A(h) \cdot \Delta h\). So wie bei einem Prisma: Grundfläche mal Höhe. Da die Scheiben so dünn sind, kann man ihre Fläche über die Höhe als konstant annehmen. Und das Volumen \(V\) des gesamten Körpers wäre dann die Summe aller Volumen der Scheiben mit einer Scheibenhöhe, die gegen 0 gehen soll. Man schreibt:
$$V = \lim_{\Delta h \to 0} \sum \Delta V = \lim_{\Delta h \to 0} \sum A(h) \cdot \Delta h = \int A(h) \space \text{d}h$$
Jede dieser Flächen mit Flächeninhalt \(A\) ist ein Polygon, also ein Streckenzug, der nur aus geraden Stücken besteht. Man kann nun - z.B. mit Hilfe der Gaußschen Flächenformel - zeigen, dass die Funktion \(A(h)\) immer ein Polynom zweiter Ordnung ist. Das musst Du jetzt nicht verstehen - glaube mir einfach, dass man hier jede Fläche mit einer Formel der Art
$$A(h) = k_2 \cdot h^2 + k_1 \cdot h + k_0$$
berechnen kann. Wobei \(k_0\), \(k_1\) und \(k_2\) konstante Größen sind. Sei nun \(f(x)\) ein Polynom zweiter Ordnung,
$$f(x) = k_2 \cdot x^2 + k_1 \cdot x + k_0$$
so hat Thomas Simpson gezeigt, dass man das Integral (das ist diese komische Summe oben) dieses Polynoms in den Grenzen von \(x=a\) bis \(x=b\) wie folgt berechnen kann: $$\int_{a}^{b} f(x) \space \text{d}x = \frac{b-a}{6} \left( f(a) + 4\cdot f \left(\frac{a+b}{2}\right) + f(b) \right)$$ Dies ist die nach ihm benannte Simpsonregel. Überträgt man dies auf das Integral für das Volumen, so ist hier
$$\begin{aligned} f(a) &= A(h=0) \\ f\left( \frac{a+b}{2} \right) &= A\left( \frac{H}{2} \right) \\ f(b) &= A( h=H) \end{aligned}$$ wenn \(H\) die Höhe des Prismatoiden ist. Die Variable \(h\) läuft natürlicherweise von der Grundfläche \(h=0\) bis zur Deckfläche \(h=H\). Eingesetzt in die Volumengleichung von oben erhält man dann
$$V = \frac16 H \left( A(h=0) + 4 A\left(h = \frac{H}{2}\right) + A(h=H)\right)$$ wobei \(A(h=0)\) die Grundfläche ist (das Rechteck im Beispiel oben), \(A(h=H)\) ist die Deckfläche (die des grünen Dreiecks) und \(A(h=H/2)\) ist die Fläche, die sich ergibt, wenn man den Prismatoiden genau in der Mitte durchschneidet, was ich mit der blauen Fläche versucht habe anschaulich zu machen.
Mit der Kenntnis dieser drei Flächen und der Höhe lässt sich dann das Volumen \(V\) nach obiger Formel berechnen.
Gruß Werner