Aufgabe:
Zu einer Wirtschaftichkeitsuntersuchung mitteis Kostenvergleichsrechnung liegen folgende Daten vor: 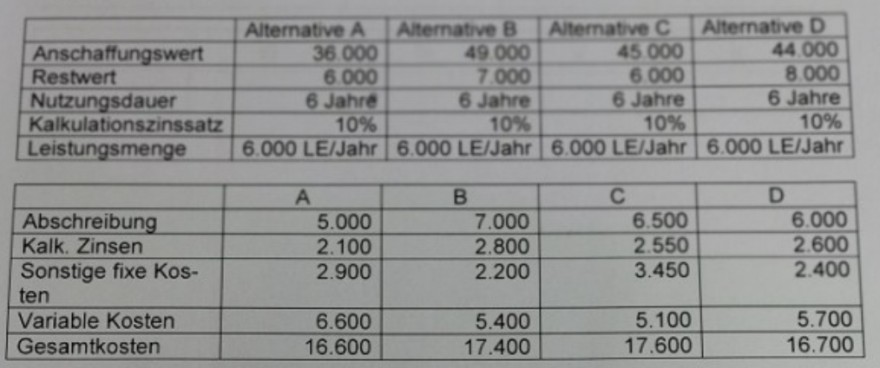
Berechnen Sie die folgenden Größen:
a) Bei welchem Kalkulationszinssatz würden \( A \) und \( D \) zu gleichen Gesamtkosten führen?
b) Bei welcher Leistungsmenge würden \( \mathrm{B} \) und \( \mathrm{C} \) zu gleichen Gesamtkosten führen?
c) Die Erlösfunktion sei \( E=1,9 x \). Bei welcher Menge \( x \) liegt für A der Break-EvenPunkt?
d) Bei welchen variablen Stückkosten von D entsprechen die Gesamtkosten von D denen von \( \mathrm{A} \) ?
e) Um wie viel müssten die Anschaffungsausgaben sinken, damit die Gesamtkosten von B denen von A entsprechen?
f) Bei welchem Verkaufspreis liegt die Gewinnschwelle für B bei einer Menge von \( 5.000 ? \)
g) Die kritische Menge zwischen B und C entspricht der Break-even-Menge von B. Wie hoch ist der Verkaufspreis von \( \mathrm{B} \) ?
h) Um wie viel müsste die Menge bei B steigen, damit die Stückkosten von B um 0,50 Euro sinken?
i) Bei welchem Restwert für \( \mathrm{C} \) würden die Gesamtkosten von \( \mathrm{C} \) denen von \( \mathrm{B} \) entsprechen?
j) Welche Alternative würden Sie im Paarvergleich zwischen A und B sowie C und D jeweils vorziehen, wenn eine Produktionsmenge größer als die jeweils im Paarvergleich kritische Menge erwartet wird.
Mein bisheriger Ansatz:
Kostenfunktionen aufstellen von B und C
K(B)=12000+0,9x
K(C)=12500+0,85x
Habe die gleichgesetzt und dann habe ich 100.000 rausbekommen.
Habe die dann in die Break-Even-Formel eingesetzt:
100.000=12000p−6.000
nach P aufgelöst und es kam 0,06 raus.
Ist aber falsch.