Berechne die Länge des Dachsparrens

Question

hallo könnte mir jemand sagen wie man sowas ausrechnet 

Answer 1

bei deinem Dachsparren handelt es sich, um ein gleichschenkliges Dreieck, dessen Grundseite und einen Winkel du gegeben hast. Das reicht leider nicht aus, um ein gleischenkliges Dreieck zu berechnen. Deswegen musst du das gleischenklige Dreieck in zwei rechtwinklige Dreiecke aufteilen:

Die Höhe, die wir eingezeichnet haben heißt Höhe h_c und teilt das Dreieck in zwei rechtwinklige Dreiecke. Die Grundseite lässt sich nun auch in zwei gleich große Teile trennen. Nun können wir mit Hilfe der Trigonometrie ganz einfach die Dachsparrenlänge bestimmen:$$ cos(\alpha)=\frac{\left(\frac{c}{2}\right)}{a} \quad | \cdot a $$$$ cos(\alpha)\cdot a=\frac{c}{2}    \quad |:cos(\alpha)$$$$  a=\frac{\left(\frac{c}{2}\right)}{cos(\alpha)}    $$ Einsetzen:$$  a=\frac{\left(\frac{12.24}{2}\right)}{cos(42)} ≈ 8.24m  $$ Nun musst du noch die 0.4m überstehenden Dachsparren mit einberechnen:$$8.24+0.4=8.64m$$

Grüße

Comments

Ja verstehe die rechnung ganz logisch wie es aussieht aber man könnte doch dann 6.12 direkt nehmen anstatt 12.24 halbe oder?

---

Ja, das kannst du.

---

Es müssen aber noch 0,4 Meter Überstand dazugerechnet werden, sind dann genauer 8,635 Meter, laut Onlinerechner.

---

Oh ja, das stimmt. Der Dachsparren ragt 0.4m noch über das Haus. Habe es in die Antwort editiert.

---

Eine frage hab ich noch kann es auch vorkommen ,dass ich tangens oder sinus benutzen muss ?

---

Oh, Antooooooooooooooooooonnnnnn, wie lange kann man denn eine Antwort hier noch ändern?

---

@MatheOpfer

Bei dieser Aufgabe kannst du nur den Kosinus verwenden mit der gegebenen Seite und dem Winkel. Es kann natürlich sein, dass du auch den Sinus und den Tangens in anderen Aufgaben brauchst, das kommt auf den Sachverhalt an.

Sinus eines Winkels= Gegenkathete/Hypotenuse

Kosinus eines Winkels=Ankathete/Hypotenuse

Tangens eines Winkels=Gegenkathete/Ankathete

---

Okay verstehe und alpha  42 grad war in dem fall die hypotenuse richtig ?

---

Dummerjohn,

Man kann seine Frage noch 20min nach der Veröffentlichung als "Normalo" bearbeiten. Moderatoren können das jederzeit.

---

Matheopfer, das ist leider komplett falsch. Ich starte nochmal meinen PC, dann kann ich dir besser helfen als am Handy... Sekunde.

---

So hier vielleicht hilft dir das:

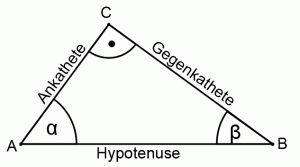
Die Hypotenuse ist immer gegenüber des 90°-Winkels im rechtwinkligen Dreieck! In deinem Beispiel:

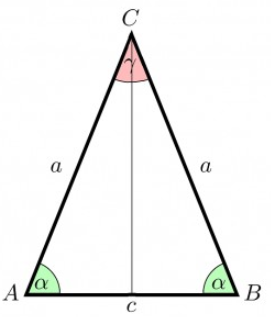
Haben wir den Winkel Alpha gegben. Die Hypotenuse ist gegenüber vom 90°-Winkel. Also die Seite a. Du musst immer vom gegebenen Winkel aus gucken, welche Seite ihm gegenüber steht. Welche Seite steht denn gegenüber vom Winkel Alpha? Das ist die Höhe, die wir eingezeichnet haben (Gegenkathe).. Was liegt denn am Winkel Alpha? Die Hälfte der Strecke von "c". (Ankathete)

Versuch mal diese Aufgabe zu lösen:

Du hast gegeben einen:

γ=90°

β=22°

a=12cm

Versuch das mal  zu lösen du hast ja ganz oben das Bild. Du darfst übrigens nicht mit dem 90 Grad Winkel rechnen.

---

Hmm das lässt sich irgendwie nicht ausrechnen a ist die hypotenuse aber welche formel soll ich dann nehmen

---

Sinus eines Winkels= Gegenkathete/Hypotenuse

Kosinus eines Winkels=Ankathete/Hypotenuse

Tangens eines Winkels=Gegenkathete/Ankathete

Die Hypotenuse ist immer gegenüber vom 90 Grad Winkel. Der ist in der Aufgabe der Winkel Gamma. Also ist "c" die Hypotenuse.

Wenn man also vom Winkel Beta aus guckt und  z.B "a" berechnen will, muss man

cos(ß)=a/c

---

Ist ist das so falsch ?

---

oder meinst du das so ?

---

Eieieii, du musst noch viel lernen. Ich muss jetzt leider schlafen und habe morgen leider nicht viel Zeit.
Dein Ziel ist es jetzt, dieses Video zu gucken und es versuchen zu verstehen:https://youtu.be/NOFCCBDtV08
Die Aufgabe, die du eingestellt hast ist schon etwas anspruchsvoller und dir fehlen offensichtlich Grundkentnisse.

---

Aber das endergebnis ist doch richtig ?

---

Nein, c≈12.94cm

---

Steht doch da beim 2ten bild unten

---

Das zweite ist richtig.

Answer 2

Man nimmt an, dass das Dreieck gleichschenklig ist. Dann teilt die Höhe die Grundseite nämlich in zwei kongruente rechtwinklige Dreiecke mit bekanntem Winkel und Ankathete, die man dann mit Trigonometrie und Pythagoras behandeln kann.