Stochastikaufgaben. Bedingte Wahrscheinlichkeit für auswärtigen Mann im Museum.

Question

Hi zusammen
die Ausstellung über den Maler David Teniers im Kunstmuseum wird zu 41% von Einheimischen besucht . Von diesen sind 43% Männer , von den auswärtigen Besuchern sind es 47%
a) wie groß ist der Anteil der Besucherinnen der Ausstellungen ?
b) der 50 000. Besucher ist ein Mann
mit welcher Wahrscheinlichkeit kommt er von auswärts ?
Tel a konnte ich lösen aber Teil b verstehe ich nicht
danke für eure Hilfe

Answer 1

 

man mache sich ein kleines Baumdiagramm:

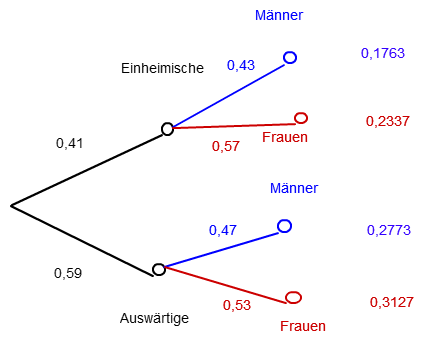
Jetzt kann man sofort ablesen:

a) 0,2337 + 0,3127 = 0,5464 = 54,64%

b) Männer sind insgesamt 0,4536 (unsere Grundgesamtheit); auswärtige Männer sind 0,2773 ("Merkmalsträger").

Also müssen wir 0,2773 durch 0,4536 dividieren: 

0,2773 / 0,4536 ≈ 0,6113 = 61,13%

Der 50000. Besucher, ein Mann, kommt also mit ca. 61,13% von auswärts. 

Besten Gruß

Answer 2

ob es sich um den ersten oder 50000-sten besucher handelt ist egal, das erscheinen der besucher ist stochastisch voneinander unabhängig.

es gilt

P(Besucher auswärtig) = 0,59

und

P(Besucher männlich | Besucher auswärtig) = 0,47

insgesamt also P(Besucher männlich ∩ Besucher auswärtig) = P(Besucher auswärtig) • P(Besucher männlich | Besucher auswärtig) = 0,59 • 0,47 = 0,2773

Comments

sorry Brucybabe hat recht, ich hatte nicht berücksichtigt, dass schon bekannt war, das es sich um einen männlichen besucher handelt.

---

man kann sich auch das inverse baumdiagramm zeichnen, das kann zum verständnis etwas beitragen:

 

rechnen lässt sich das dann über die schnittwahrscheinlichkeit:

P(Einheimische ∩ Männer) = P(Männer) • P(Auswärtige|Männer)

0,2773 = 0,4536 • P(Auswärtige|Männer)

P(Auswärtige|Männer) = 02,773 / 0,4536 ≈ 0,6113