Zur Geometrie
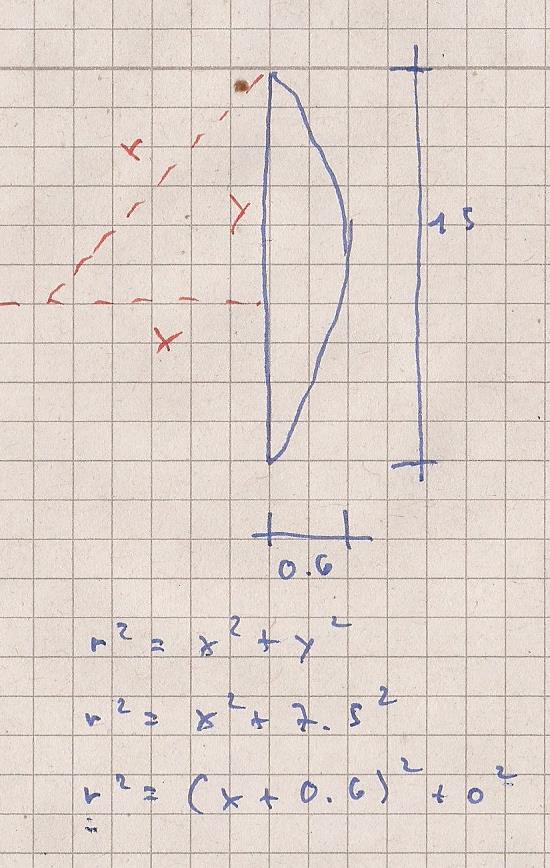
r^2 = r^2
x^2 + 7.5 ^2 = ( x + 0.6 ) ^2 + 0 ^2
x = 46.575
r = x + 0.6
r = 47.175 cm
Kreisfunktion
y = √ ( r^2 - x^2 ) = f ( x )
Kreisscheibe ( Schnitt an beliebiger Stelle )
A ( x ) = [ f ( x ) ] ^2 * π
A ( x ) = [ √ ( r^2 - x^2 ) ] ^2 * π
A ( x ) = ( r^2 - x^2 ) * π
Stammfunktion
S ( x ) = ∫ A ( x ) dx
S ( x ) = π ∫ r^2 - x^2 dx
S ( x ) = π * ( r^2 * x - x^3 / 3 )
Volumen der halben bikonvexen Linse
V ( x ) = [ S ( x ) ] zwischen 46.575 und 47.125
V ( x ) = [ π * ( r^2 * x - x^3 / 3 ) ] zwischen 46.575 und 47.125
V = 53.13 cm^2
So weit so gut.
Alle Angaben ohne Gewähr.
zu tun
Volumen verdoppeln da bikonvex
und mit spez.Gewicht multplizieren
Bei Bedarf nachfragen.
mfg