Auf welcher Kurve bewegt sich eine Ecke dieses Vielecks bewegt, wenn man die Diagonale...? Geometrischer Satz?

Question

EDIT: Originalfrage:

Begründe mithilfe eines bekannten geometrischen Satzes, auf welcher Kurve sich eine Ecke des Vierecks bewegt, wenn man die Diagonale durch diesen Eckpunkt um M dreht und die andere Diagonale fest lässt.

Satz zur Aufgabe gesucht !?

 ich soll mit der Hilfe eines Satzes ( eines geometrischen Satzes ) erläutern, auf welcher Kurve sich eine Ecke dieses Vielecks bewegt, wenn man die Diagonale durch diesen Eckpunkt um den Punkt M dreht und die andere Diagonale an Ort und Stelle lasst .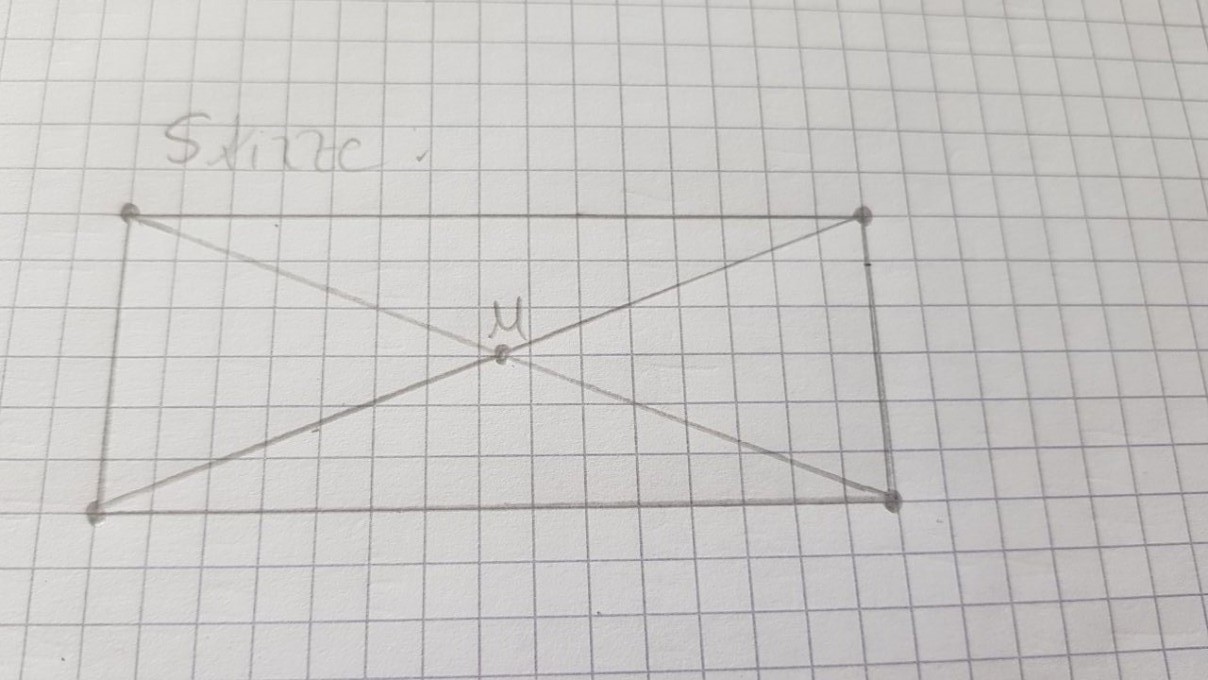 

Entweder ich verstehe die Aufagebenstellung falsch oder ist es eine runde Kurve, was meint ihr und um welchen Satz handelt es sich dann ?

Ich würde mich sehr freuen wenn ih in der Lage wäre mir weiter zu Helfen.

Danke

Comments

Ich kann mir leider nichts vorstellen.
Um welchen Punkt soll das Rechteck
gedreht werden ?
- um einen Eckpunkt
- um den Mittelpunkt

---

Begründe mithilfe eines bekannten geometrischen Satzes, auf welcher Kurve sich eine Ecke des Vierecks bewegt, wenn man die Diagonale durch diesen Eckpunkt um M dreht und die andere Diagonale fest lässt.

so lautet die Aufgabe wortwörtlich, hoffe du kannst mir nun eventuell weiter helfen.

---

"auf welcher Kurve sich eine Ecke dieses Vielecks bewegt, wenn man die Diagonale durch diesen Eckpunkt um den Punkt M dreht"

Dieser Satzteil gibt keinen Sinn. Bitte Originaltext wörtlichg abchreiben.

---

habe ich nun, ist im Kommentar von mir zu sehen :-) und hast recht es macht keinen Sinn wie ich es geschrieben habe.

---

Also genau so ist die Aufgabe gestellt

---

Stand die Aufgabe in einem Mathebuch oder an der Tafel?

---

Wurde uns von Dozenten selbst auf geschrieben

---

Lu hat offenbar verstanden, was gemeint ist (s.u.).

Answer 1

Begründe mithilfe eines bekannten geometrischen Satzes, auf welcher Kurve sich eine Ecke des Vierecks bewegt, wenn man die Diagonale durch diesen Eckpunkt um M dreht und die andere Diagonale fest lässt.

Ja. Das ist ein Kreis.

Der Kreis liegt in der Ebene, die senkrecht zur festgehaltenen Diagonalen steht und durch eine Ecke geht, die bewegt wird.

Ein Satz dazu wäre: Alle Punkte in einer Ebene, die von einem gebenen Punkt denselben Abstand haben, liegen auf einem Kreis. Kennt ihr so einen Satz? Oder allenfalls etwas zu in dieser Richtung zu Kugeln und Schnittmengen von Kugeln?

Comments

super danke, vielleicht kommt ja nun einer den "berühmten"Satz dazu :-)

---

Kennt ihr so einen Satz? Oder allenfalls etwas zu in dieser Richtung zu Kugeln und Schnittmengen von Kugeln?

Mit ihr ist deine Klasse / dein Schulbuch ... gemeint. Allenfalls auch:

https://de.wikipedia.org/wiki/Kugel#Kugelschnitte

---

nein leider haben wir dazu noch nichts gemacht.

---

Bin gerade über diese alte Frage mit Antwort gestoplert. https://www.mathelounge.de/61434/kugelgleichungen-subtrahiert-voneinander-schnittebene

Die beiden Ecken auf der festgehaltenen Diagonalen sind Kugelmittelpunkte. Die Radien sind die Seitenlängen des Rechtecks. Nun geht es um einen Kreis der in der Schnittebene der beiden Kugeln liegt.