Leiter im Ganz mit Ecke. Sehr schwere Textaufgabe mit maßstäbelicher Zeichnung

Question

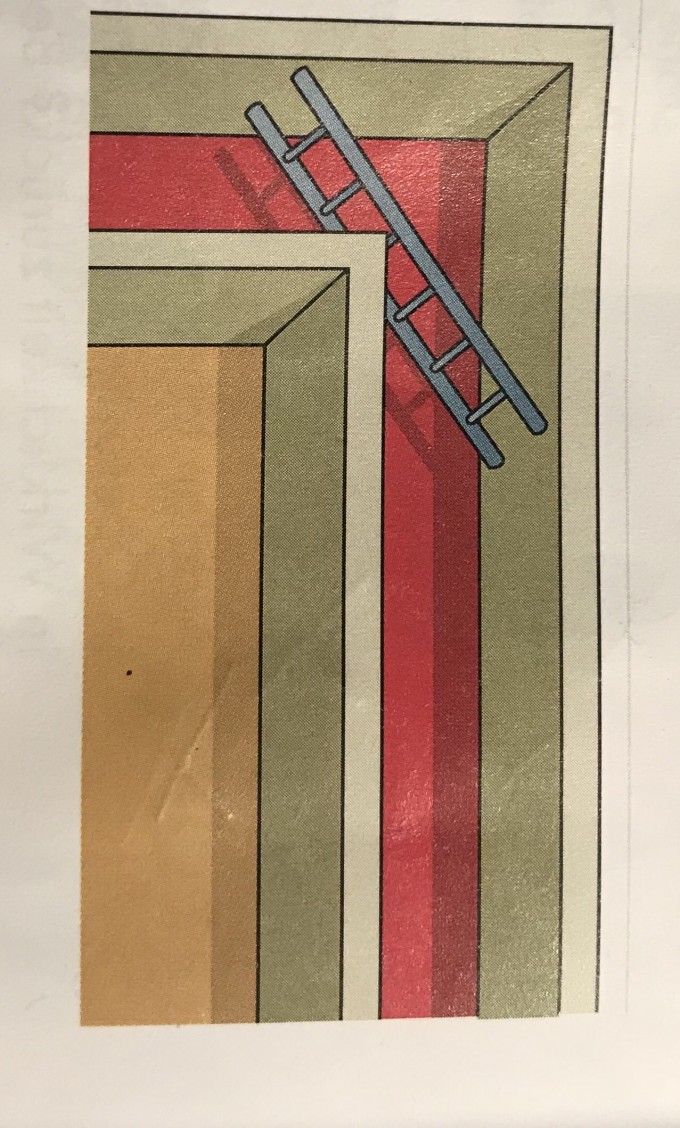
Wie lang darf eine Leiter sein, damit man sie in diesem Gang (Breite 4 m) um die Ecke bringt? Mach eine ebene maßstäbeliche Zeichnung und versuche durch Probieren mit unterschiedlich langen „Modellleitern“, um die Ecke zu biegen!Die Leiter muss immer parallel zum Fußboden sein. Erkläre, wie du vorgehst.

Ich hoffe mir hilft jemand;)

Comments

Das Bild oben ist doch schon mal ein guter Ansatz !

Answer 1

Du zeichnest den Gang mit 4 cm Breite
und machst dir Stäbe mit 4 cm, 5 cm, 6 cm
Länge usw und möglichst geringer Breite.
Dann versuchst du mit den Stäben um die
Ecke zu kommen und dabei innerhalb des Ganges
zu bleiben.
So kannst du dich an die längste Länge herantasten.

Answer 2

Man könnte Flur und Leiter in ein Koordinatensystem legen:

Die Schar aller Geraden durch (4|4) hat dann die Gleichung y=mx+4-4m  mit dem y-Achsenabschnitt 4-4m und der Nullstelle 4-4/m. Die Länge l der Leiter berechnet sich nach Pythagoras als l=√((4-4m)²+(4-4/m)²). Dann ergibt sich für jedes m eine Leiterlänge,aber nur die kürzeste passt um die Ecke.

Comments

Morgen Roland,
was bedeutet " 4-4 m " ?
mfg Georg

---

basierend auf der Tatsache das das
Maximum der Leiterlänge bei einem
Dreieck von 45 ° gegeben ist ( Symmetrie )
dürfte  die rechnerische Lösung sein

zunächst die Geradengleichung
y = -1 * x + b
4 = -1 * x + b
b = 8 m

Dreieck
l^2 = 8^2 + 8^2
l = √ 2 * 8

---

Georg.

Die Schargleichung y=mx+4-4m nennt alle Geraden, die durch (4|4) gehen und die Steigung m haben. Für jedes m ist 4-4m der y-Achsenabschnitt einer Geraden aus der Schar.