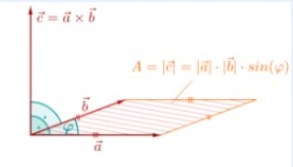
Also ich habe folgende Formel gefunden, die die graphische Bedeutung des Vektorprodukts veranschaulicht: Ich verstehe nicht wieso der Betrag des Vektorprodukts aus a und b gleich dem Produkt ihrer Längen mal sinus (phi) ist. Wie kann man sich das erklären, dass dieser Zusammenhang gilt? Aus der Abbildung werde ich leider nicht schlau. Wann kann man diese Formel ausnutzen?
\( \vec{a}=\left(\begin{array}{l}{a_{1}} \\ {a_{2}} \\ {a_{3}}\end{array}\right) \) und \( \vec{b}=\left(\begin{array}{l}{b_{1}} \\ {b_{2}} \\ {b_{3}}\end{array}\right) \) definiert als
\( \overrightarrow{\boldsymbol{a}} \times \overrightarrow{\boldsymbol{b}}=\left(\begin{array}{l}{a_{2} b_{3}-a_{3} b_{2}} \\ {a_{3} b_{1}-a_{1} b_{3}} \\ {a_{1} b_{2}-a_{2} b_{1}}\end{array}\right) \)
Der dadurch erhaltene Vektor \( \overrightarrow{\boldsymbol{c}} \) steht auf \( \overrightarrow{\boldsymbol{a}} \) und \( \overrightarrow{\boldsymbol{b}} \) senkrecht \( (\overrightarrow{\boldsymbol{c}} \perp \overrightarrow{\boldsymbol{a}} \text { und } \overrightarrow{\boldsymbol{c}} \perp \overrightarrow{\boldsymbol{b}}) \)
Er hat die Länge \( |\vec{c}|=|\vec{a} \times \vec{b}|=|\vec{a}| \cdot|\vec{b}| \cdot \sin (\varphi), \) wobei \( \varphi \) der Winkel ist, den \( \vec{a} \) und \( \vec{b} \) aufspannen. Dies entspricht dem Flächeninhalt des von \( \vec{a} \) und \( \vec{b} \) aufgespannten Parallelogramms.