(a)
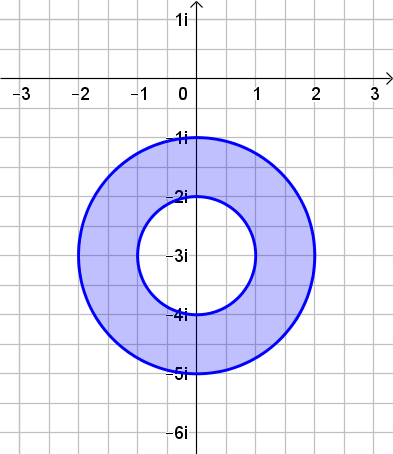
Die Gleichung bedeutet, dass der Abstand von \(-3\text{i}\) mindestens \(1\) und höchstens \(2\) ist. Man erhält einen entsprechenden Kreisring als Menge.
(b)
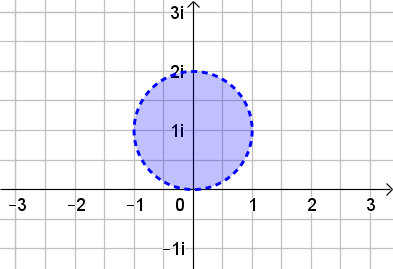
Der Abstand von \(\text{i}\) ist kleiner als \(1\) es handelt sich also um eine offene Kreisscheibe mit Radius \(1\) um den Mittelpunkt \(\text{i}\)
(c)
Keine Ahnung, ob ich richtig interpretiere was da steht. Wenn nicht solltest du das doch bitte etwas verständlicher aufschreiben. Ich denke mit "z /= 0" ist \(z\ne 0 \) gemeint und mit "'ź" ist die zu \(z\) komplex konjugierte Zahl \(\overline{z}\) gemeint.
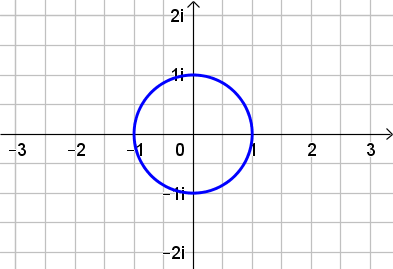
Dann kann man \(\overline{z} = \frac{1}{z}\) zu \(\overbrace{\overline{z}\cdot z}^{=\lvert z\rvert^2} =1 \) umformen und damit dann zu \(|z| = 1\). Es handelt sich also um die Kreislinie mit Radius 1 um den Ursprung.
(d)
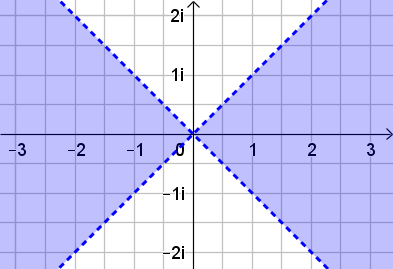
Man könnte \(z\) durch \(x + \text{i} y\) mit \(x, y\in\mathbb{R}\) ersetzen. Dann ist \(z^2 = (x+\text{i}y)^2 = x^2 - y^2 +2 x y \text{i}\). Damit wird die Bedingung \(\text{Re}(z^2)>0\) zu \(x^2 - y^2 > 0\). So erhält man dann \(x^2 > y^2\) und daraus \(\lvert x\rvert>\lvert y \rvert\).