Der Beweis ist mir noch nicht gelungen, aber ich habe Indizien dafür, dass der gesuchte Punkt y konstruiert werden kann, indem man zunächst den Schnittpunkt S der Seitenhalbierenden konstruiert und dann von Punkt X aus eine Gerade g durch S legt. Der Schnittpunkt dieser Geraden g mit derjenigen der beiden anderen Dreieckseiten, auf die sie trifft, ist (vermutlich) der gesuchte Punkt y.
Indizien:
Wenn X genau in der Mitte der der Seite AB liegt, dann stimmt die so konstruierte Gerade g mit der Seitenhalbierenden der Seite AB überein.
Wenn X genau auf Punkt A liegt, dann stimmt g mit der Seitenhalbierenden der Seite BC überein.
Und wenn X genau auf Punkt B liegt, dann stimmt g mit der Seitenhalbierenden der Seite AC überein.
In allen drei Fällen ist g also Seitenhalbierende und teilt daher jeweils das Dreieck in zwei flächengleiche Teile. Es drängt sich auf, anzunehmen, dass dies auch dann gilt, wenn X zwischen den Punkten A und B liegt.
Ich werde versuchen, einen Beweis zu finden ...
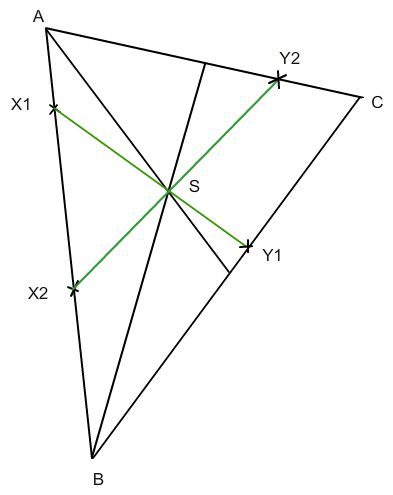
Hier noch eine Skizze mit zwei Punkten X1 und X2 und den gemäß der beschriebenen Konstruktion entstandenen Punkten Y1 und Y2. Die grün gezeichneten Geraden sind die Geraden g, die "im Verdacht" stehen, das Dreieck ABC zu halbieren.