Rechtwinkliges Dreieck: Ein Winkel und eine Seite ist gegeben

Question

 seite c = 4cm und winkel  α 40°

wie berechnen ich jetzt Seite b und a?

EDIT: Annahme: Rechtwinkliges Dreieck in der Überschrift und Tags ergänzt. 

Comments

hmm, das ist schwer zu sagen, mach mal eine Zeichnung

Answer 1

Hallo

 geht es um ein rechtwinkliges Dreieck? dann ist eines mit sin das andere cos auszurechnen , sieh dir an, wie ihr sin nd cos definiert also beschrieben habt. c ist die Hypotenuse.

Gruß lul

Answer 2

c = 4cm und winkel  α 40°
Falls die Standardbeschriftung für Dreiecke
vorliegt ist
sin ( 40 ) = a / c = a / 4
a = 2.57 cm

cos ( a ) = b / c
cos ( 40 ) = b / 4
b = 3.06 cm

Comments

meine lösungen sagen ,dass b 5,2 cm ist und a 3,4cm

---

Ist eine Skizze gegeben ?

c = 4 cm und winkel  α 40°
Wenn nur 1 Seite und 1 Winkel gegeben sind
bleibt als Lösung nur ein rechtwinkliges
Dreieck.

c ist üblicherweise die Bezeichnung für die
Hypotenuse. Dies ist dann die längste
Seite im Dreieck.
b und a als Katheten dürfen ncht länger sein.

---

Nach den Angaben von FaceMan müsste das Dreieck so aussehen:

Die Seiten \(a=|CB|\) und \(b=|CA|\) sind

$$\begin{aligned} a &= \frac{4 \text{cm}}{ \cos (40°)} \approx 5,22 \text{cm} \\ b &= 4 \text{cm} \cdot \tan(40°) \approx 3,36 \text{cm} \end{aligned}$$

---

Ich dachte mir schon das die Zuordnung von
Bezeichnung zu real eine andere sein würde war
aber zu faul dies auszuprobieren.

Dies ist die Standardbezeichnung für ein Dreieck.

Dabei soll es auch bleiben.

---

Hallo Georg,

Ja - Du hast Recht. Ich war etwas ungenau.

... müsste das Dreieck so aussehen:

das stimmte wohl nicht so ganz. Besser ist wohl diese Darstellung:

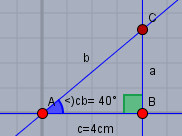
dann stimmt das auch mit Deiner Vorgabe überein. Ich vermute, dass es heute durchaus üblich ist, den rechten Winkel in \(\alpha\) oder \(\beta\) zu plazieren. Dann müssen die armen Schüler das Dreieck im Kopf nicht drehen, wenn sie Aufgaben von der Art 'Du siehst die Spitze des Turms unter xy°, wie hoch ist der Turm' lösen müssen.

---

Hallo Werner,
mein letzter Beitrag war nicht als Kritik
an deiner Lösung gedacht.
Du hast die Seitenlängen doch richtig
berechnet.
Ich wollte nur darauf aufmerksam machen
das ich mich bezüglich der Bezeichnungen
von Eckpunkten, Seiten und Winkeln im
Dreieck nicht mehr ändere.

mfg Georg

---

Das rechtwinklige Dreieck wurde damals in der
Realschule am Thaleskreis erklärt.
Deshalb ist der rechte Winkel bei mir immer
oben.

---

mein letzter Beitrag war nicht als Kritik an deiner Lösung gedacht.

Das hatte ich auch nicht so verstanden. Das war eher 'ne Eigenkritik.