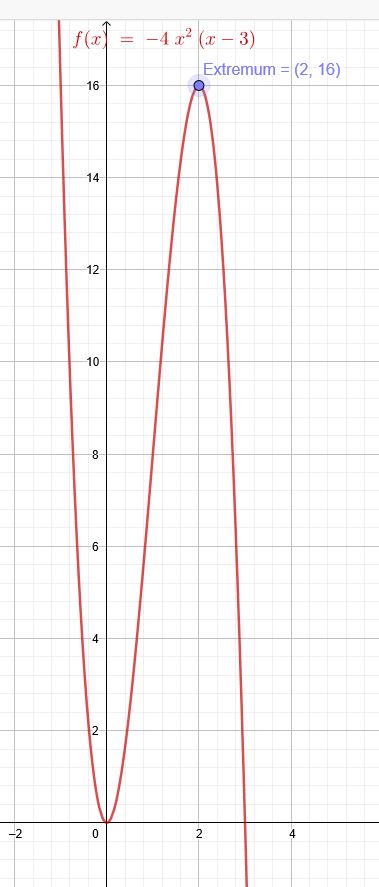
Eine Parabel 3. Ordnung berührt die x-Achse im Ursprung, hat ein Extremum bei \(x=2\) und schließt im 1.Quadranten mit der x-Achse eine Fläche vom Inhalt \(A=27\) ein. Wie heißt die Gleichung dieser Parabel?
\(f(x)=a•[x^2•(x-N)]\)
\(f´(x)=a•[2x•(x-N)+x^2•1]\)
\(f´(2)=a•[2•2•(2-N)+2^2]=a•[4•(2-N)+4]=0\) → \(N=3\)
\(f(x)=a•[x^2•(x-3)]=a•[x^3-3x^2]\)
\(27=\int\limits_{0}^{3}a•[x^3-3x^2]dx\)
\(\frac{27}{a}=[\frac{x^4}{4}-x^3]_0^3=\frac{81}{4}-27=-\frac{27}{4}\)→\(a=-4\)
\(f(x)=-4•x^2•(x-3)\)